First steps with a big impact

Hello again!
With the third week of work in the books, it’s high time for another update here. We’ve been busy getting everything set up on ARCHER2 to be ready to run proper simulations and get into the performance measurement of the MPAS atmosphere model.
After some technical issues with downloading and compiling MPAS during the first week, we set our eyes on writing scripts to help automate future runs. As we intend on simulating a wide variety of scenarios using different parameters such as mesh size, model run time and number of nodes used, not having to manually change these for each run will save a lot of time in the future.

Last week we were finally were able to start running the first simulations. This wasn’t a real test scenario yet but a simple idealized case. Figure 1 shows the result of a Jablonowski & Williamson baroclinic wave modelled for 150 hours (just over 6 days) propagating across the Earth. This is a very simple test often used to see whether an atmospheric model fundamentally works. It models a single pressure wave propagating zonally across the Earth.
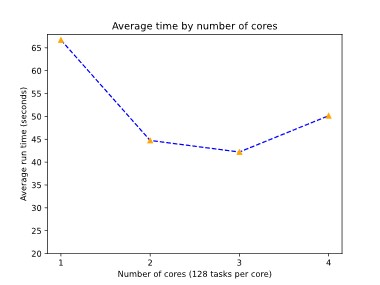
While not very exciting to look at, these kinds of tests help us to see whether MPAS is working properly and also gives us an important insight into how we can best design our upcoming experiments to make the best use of our time and computing budget. It also gives us a first look at the performance of the MPAS atmosphere model. As seen in the Figure, the average run time dropped from 1 to 3 cores, showing better performance with more computing power, but increased again when 4 cores were being used. This is most likely due to any performance gain by further parallelization of the model being diminished by more time spent in communication between the tasks. These are the kind of insights that we hope to find later in our performance analysis, but on a much bigger scale, and will investigate using profiling tools to pinpoint where performance is lost.
With the experiences gained from the last few weeks, we are now ready to start the proper performance analysis of MPAS, next up is debugging some of the automation scripts and running small scale simulations for our first real scenario. So, stay tuned for more updates!

Hi Jonas, interesting mesh! Not only, because I’m a fan of the smart game “settlers of catan” (in a much easier scale), but also because I immediately asked myself, why the grid is hexagonal.
The hexagon is easier to calculate than several circles (ideal “points” for masurement or replaced by calculations in your case). Several hexagons are addable to an area covering the whole globe, etc.
BUT, a hexagon is not devidable into other hexagons. A drawback may be, that you can’t easyly test the best scale of your model by deviding one “cell” into some more cells, as it is possible for quadrats (4 more – or 9 if you want to store the same centre) or triangles (4 more with the same centre, but partly different orientation in space).
STOP! I have to slow down my thinking about geometry now – you might have a good answer for me concerning geometry of the cells. Thank you!
Hello Oliver,
You’re right, the hexagon is able to regularly tile the entire globe and this is indeed what you see in the regular meshes that MPAS uses. This is somewhat of a coincidence though, since MPAS doesn’t define the cells through a regular shape but as centroid Voronoi tessellations. So a central point is defined and the cell then covers the area that is closest to that point (here is a fun web app that shows how they work http://alexbeutel.com/webgl/voronoi.html). Instead of needing to subdivide the hexagons themselves we can ‘add’ more points and in that way scale the problem size. So to achieve a halving of the cell sizes in the regular mesh (thus doubling the resolution) we need four times the amount of points/cells.
Interestingly enough, for MPAS we found that indeed the most important thing in performance is the number of cells and not their size, so a refined mesh which has a region of very small cells in one region (thus a high resolution there) can be compensated in performance by using a coarser resolution away from it.