Implementation of an advanced STAbility condition of explicit high-order Spectral Element Method for Elastoacoustics in Heterogeneous media

Project reference: 2209
The numerical simulation of wave propagation phenomena is of great interest in many areas of science and engineering, including seismic and acoustic applications. In this context, the use of time-domain solvers enables to significantly reduce the memory requirements and the need to devise effective preconditioners, when compared to frequency domain solvers. The efficiency of a time-domain simulation using explicit time marching algorithms is directly linked to the stability limit of the selected time marching scheme (i.e. the time stepΔt), especially for long simulations: the larger Δt assuring stability, the lower the number of iterations required. In the Spectral Element Method (SEM, a finite element method with high-order polynomials) the classical stability condition (i.e. the Courant Friedrichs Lewy condition, CFL) depends on the polynomial order and it can be estimated for homogeneous domains and structured mesh only. The CFL condition reads:
α=c Δt / h ⩽αm
with c being the wave speed andhthe characteristic element size.
Previous analyses revealed instabilities are often observed when the CFL stability limit derived for homogeneous materials is adapted to heterogeneous media by simply using the lowest local velocity. This inconvenient leads to apply arbitrary safety factor to αm, ending up in extremely small Δt(~10-6 s).
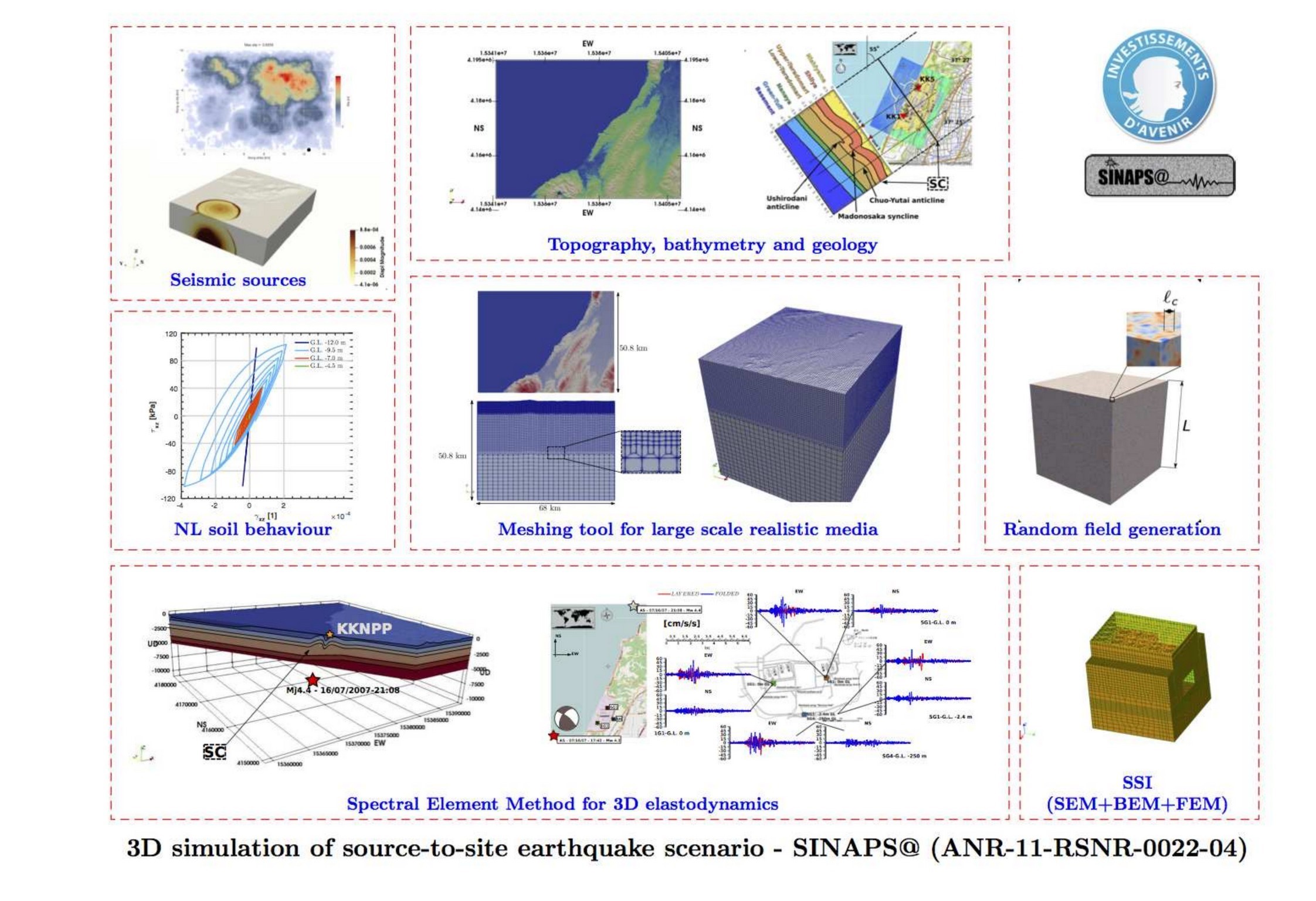
The objective of this work is to implement an advanced stability criterion that is accurate for heterogeneous elastic and acoustic media, in a HPC wave propagation solver based on the spectral element method, called SEM3D. The latter is an efficient HPC software, based on a spatial domain decomposition scheme for parallel distributed-memory resolution and it includes a large-scale random field generator to add randomly distributed heterogeneity to the problem at stake. SEM3D runs in production phase and it has been widely tested on several supercomputers and on 10000+ CPU cores.
The internship will be focused on implementing an element-wise stability criterion in SEM3D, that accounts for the local material heterogeneity (non-periodic) but that conditions the whole simulation. This challenging task resorts to solve as fast as possible several element-wise eigenvalue problems on each domain partition, without assembling the local mass and stiffness matrices. Advanced algebraic libraries will be employed. Based on the advancements, the work can be extended to the implementation of an element-wise time-marching scheme with different time-stepping (and accuracy) based on the local stability condition.
The development and testing phase will be done on the Mésocentre Moulon supercomputer facilities, where SEM3D is already compiled.

Computing a local stability condition for heterogeneous elastoacoustic problems, in a domain decomposition parallel scheme.
Project Mentor: Filippo Gatti
Project Co-mentor: Régis Cottereau
Site Co-ordinator: Karim Hasnaoui
Learning Outcomes:
The intern(s) will be learning how the spectral element method is implemented in a modern HPC environment, as well as to implement an advanced stability condition by solving an eigenvalue problem via advanced parallel schemes.
Student Prerequisites (compulsory):
Student of Engineering or Physic
- Background on the Finite Element Method and applied math
- Basics in coding for scientific applications
Student Prerequisites (desirable):
- MPI/OpenMP
- fortran90/C++
Training Materials:
https://onlinelibrary.w iley.com/doi/abs/10.1002/nme.5922
https://igpppublic.ucsd.edu/~shearer/227C/spec_elem_monograph.pdf
Workplan:
- Week 1: Training on SEM3D (including automated non-regression testing) + literature review
- Week 2: feasibility study, testing available libraries for eigenvalue problem resolution to be linked to SEM3D
- Week 3: Plan redaction and submission, construction of a suite of case studies
- Week 4-6: Implementation of stability condition for acoustic problems (student 1) and for elastic problems (student 2)
- Weeks 7: Extensive test on the defined case studies and on automated non-regression test cases
- Week 8: Final Report editing and submission
Final Product Description:
At the end of project, SEM3D is expected to be running on extremely large and heterogeneous elastoacoustic set-ups with the largest time step possible, according to the element-wise stability criterion computed beforehand.
Adapting the Project: Increasing the Difficulty:
Implement different time-marching schemes depending on the stability
Adapting the Project: Decreasing the Difficulty:
Implement the element-wise stability condition on acoustic problems only.
Resources:
The project is entirely based on SEM3D, which is proprietary code and that will be delivered to the student. The project will be conducted by exploiting the computational resources of the Mésocentre Moulon (http://mesocentre.centralesupelec.fr/), the pool of supercomputer resources of CentraleSupélec and ENS ParisSaclay. An account will be assigned to the student by the time the project starts. Student(s) will connect remotely via ssh to the supercomputer facility, with no limitation (within the common user’s policy).
SEM3D is already compiled and it has been extensively tested on the Mésocentre Moulon supercomputer facilities, which include dedicated nodes for visualization and post-processing.
Organisation:
IDRIS, CentraleSupelec

