Keeping it simple with Deustch Jozsa’s algorithm.
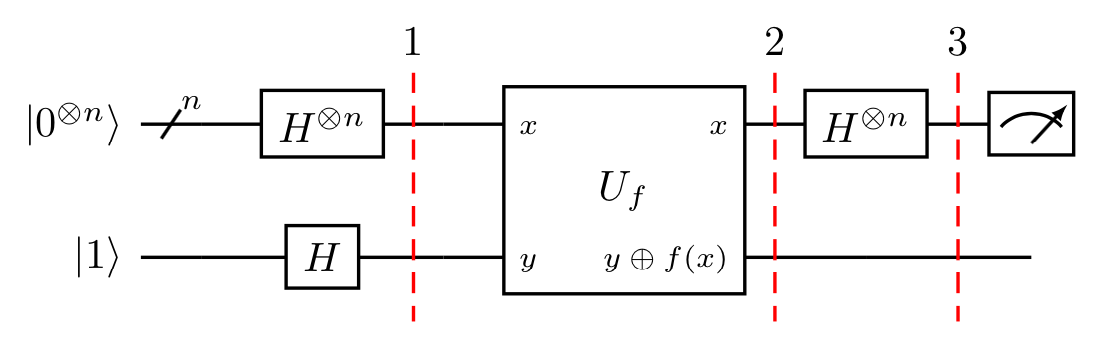
The Deustch Jozsa algorithm stands out as one of the first quantum algorithms that performs better than the best classical algorithm. It is a simple and elegant algorithm that originated from the Deustch algorithm (for a single cubit) and was generalised to several qubits.
So what’s the problem we want to solve?
We are given a unknown Boolean function i.e. given a string of bits it returns either 0 or 1,
and this function is either balance or constant, meaning that a constant function will return 0’s or 1’s and a balance function will have 0’s for half of the inputs and 1’s for the other half. Is our function f balanced or not?
Solution:
In a classical computer in the best case scenario we would need at least 2 queries to the oracle to determine whether the function is balanced or not. In the worst case we need half the number of inputs plus one. The power of quantum computation lies in the fact that with a single query to the oracle we are able to know if our function is balanced or not.
Our function implemented in the oracle is described as follows
where is addition modulo 2.
So let’s describe the algorithm!
- We get two quantum registers, one with n qubits initialized to
and a single qubit initialized to
.
.
- We apply a Hadamard gate to each state to create superposition state.
.
- We apply the quantum oracle that goes as follows:
- We then apply a Hadamard gate to each qubit in the first register.
- The last step is that we measure the first register.
which evaluates to 1 if
is constant and to 0 if
is balanced.
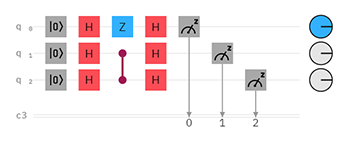
Example circuit
Choosing and
where f(x) is balanced. The implementation of the algorithm on a circuit would look like:

Leave a Reply