Make runtime of your app and life shorter, vectorize!

Vectorization is a first step in optimization process to produce high performance algorithms. Moti and I contended with vectorization for a few days. As mentioned in one of our previous posts, we decided to implement SIMD vectorization using Intel SSE/AVX instructions into our C/C++ code.

Auspicious beginning

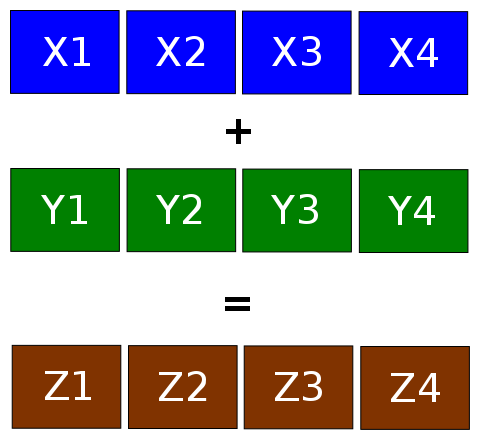
The core of K-Means clustering, is based on distance measurement between two points. And for a dataset of 100k of points this becomes arithmetically intensive, while a very vectorized and parallel operation. So, we have a great opportunity to try some simple vectorization. The target is a simple function for computing distances between two points in 6-dimensional space (each point is a vector of 6 elements). To save precious cycles, we actually compute the squared distance between two points, d = ||p – q||^2, what corresponds directly with a dot product.

Vectorization for double-precision. Three chunks of 2 numbers.

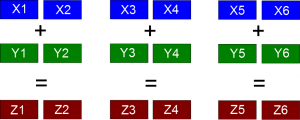
The original dataset is stored as double-precision numbers (double). SSE/AVX can operate with 2 items of double at each step (extended to 4 in recent versions). It means that for 6 dimensions we have to split vectors into 3 chunks (see figure).

Our implementation is in C/C++. To introduce vector support in our codes one option is to use assembly code (NO!!) or use intrinsics by including a standard Intel header file: immintrin.h.

You can see simple function for computing distances using dot product:

double PointDistSq(double *p, double *q)
{
// load p
__m128d p_1 = _mm_load_pd(p);
__m128d p_2 = _mm_load_pd(&p[2]);
__m128d p_3 = _mm_load_pd(&p[4]);

// load q
__m128d q_1 = _mm_load_pd(q);
__m128d q_2 = _mm_load_pd(&q[2]);
__m128d q_3 = _mm_load_pd(&q[4]);

// Compute dot product of the difference between the p1 and p2
// in each dimension.
__m128d diff_1 = _mm_sub_pd(p_1, q_1);
__m128d diff_2 = _mm_sub_pd(p_2, q_2);
__m128d diff_3 = _mm_sub_pd(p_3, q_3);

// The flag 0xFF instructs the CPU to perform full dot product.
__m128d dp_1 = _mm_dp_pd(diff_1, diff_1, 0xFF);
__m128d dp_2 = _mm_dp_pd(diff_2, diff_2, 0xFF);
__m128d dp_3 = _mm_dp_pd(diff_3, diff_3, 0xFF);

// Add all subproducts
__m128d final = _mm_add_pd(_mm_add_pd(dp_1,dp_2),dp_3);

// Extract result.
double result = _mm_cvtsd_f64(final);
return result;
}

After such a simple vector implementation we got very nice speedup for this function, about 2.5. But only in case when all bytes are on right position. If not, you can easily get a segmentation fault. But more about it later.

An interesting note: we converted an operation performed on one element at a time to operate on 2 (vector of size 2), so the theoretical speedup one would expect to achieve is 2 or less. So how can we explain 2.5? (No cheating). The fact is that memory throughput was also improved, loading 2 elements at once is better than 1 every time. Nice :).

Vain attempt

The next step was to try vectorize another very used function in our code. Unfortunately that function was more complicated and contained branching, if statement, where in one branch we want add two components of the vector and in the second branch we want to subtract them.
Branching is no good for human kind and vector systems. To avoid this if statement and to preserve SIMD philosophy a solution could be to create mask that contains numbers 1 or -1. Using that we can multiply the second number by this mask and for all data do the same operation: +.

This implementation was more complex and contained much more lines, but finally worked. When writing worked, I mean that vectorized and original function returned the same results. But, for this vectorization we didn’t get any speedup, vice versa, the vectorized function was even slower. Doesn’t matter, it took only about two hours of my work. And because I am pround of my work I will just put my vectorized code in comments.

Easy continuation with unforeseen troubles

Following detailed study of the original k-means code, we figured that single-precision (float) can be used instead of double, it can improve performance by a lot. So, we went on to switch our application into single-precision instead of double-precision.

It means that vectorization has to be converted for single-precision as well. With native support for vectors of 4 elements we would expect that performance will be even better.

So now we have basically two variants of how to handle 6-dimensional vectors. We can maintain the model with 3 chunks of 2 numbers used for double-precision (right picture), or we can use the model shown on the left picture, which can be more effective because we need only 2 chunks and it means less operations. In any case we should fill the unused registers by zeros to avoid computational complications (dot product, finally adding over all coordinates, etc.).

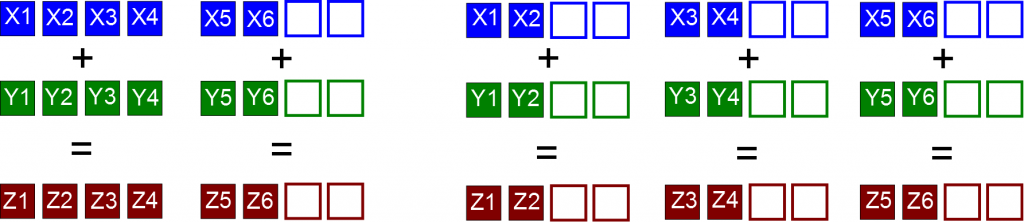
Vectorization for single-precision. Two options: 2 chunks (4+2) or 3 chunks (2+2+2).

The conversion to single-precision was done (using model with only 2 chunks) and everything worked perfect. I had very good feeling from this work. But after some little changes to the code, which seemingly weren’t connected with any vectorized part, suddenly the program crashed with segmentation fault. Friday the 13^th, what a horror.

After an hour spent by staring, removing new changes, compiling, running, re-adding new changes, compiling, running and getting the same segmentation fault I was really sad and tired. I wanted to quit with vectorization, because without it everything worked fine. But still, I was curios about that mysterious error, what is wrong? No way, I have to use some debugger to get more information, because these two words “segmentation fault” can say many things!

Is it better to solve a problem when you know where it is

After some debugging I found out that problem is really in vectorization, something is wrong with loading data, they aren’t correct, but why?? Here I was really at the end of my possibilities to solve this problem. Fortunately, Moti already knew what I didn’t. The answer to my question was data structure alignment.

Let me explain it: Data structure alignment is the way how data are arranged and accessed in computer memory. When a computer reads from or writes to a memory address, it does this in constant size chunks, called word. Word is the smallest number of bytes computer works with. For 32-bit architecture it is 4 bytes. It means, that data to be read should be at a memory address in some multiple of 4. And when it is not the case, e.g. the data starts at the 14th byte instead of the 16th, then the computer has to read two 4-byte chunks and do some extra calculation before the requested data has been read.

In some special cases (where alignment is strictly required) it may generate a fault. Vector data operations are one such case, and what is exactly the case of my vectorization problem. Because what I did was, adding some new variables into an internal data structure. Finally when I know what is wrong, I can easily fix it. The only thing that has to be done is add some meaningless bytes in my data structure, called padding, to make them correctly aligned in memory.

Tradaa … now everything works again :).