Quiz – clustered data using k-means
Moti and I work on the k-means clustering project, you can read our first post about it. Now we prepared a short and easy quizz related with k-means topic for you.
When you cluster dataset using classic k-means algorithm you get clusters (coloured points) like you can see on pictures.
- This diagrams have a specific name, what is it?
- Why is the shape like a polygon with a straight lines? We would expect them to be circles.
- What is the shape to expect the more centers we ask?
HPC students, your answers write to comments :). The first full correct answer will be awarded!
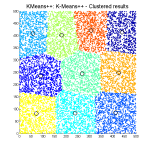
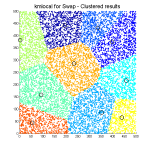
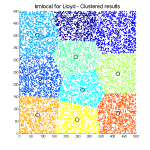

Can I start with answering the second and the third part first? I am still not sure about the first question.
I think the answer to the second question is quite easy. Consider the case of only two clusters, then the separation line will be a straight line normal to the connection line between the cluster centres and hitting it in its middle point. All points on the one side are closer to the first centre, all points on the other side closer to the other centre. Following from that, adding more centres will result in clusters which have more and more straight lines as boundaries. Am I right, or did I get the question wrong?
1) Looks like a Voronoi diagram – a memory of listening to a seminare by a dutch computational physicist (or mathematician, can’t recall) faintly emerges from somewhere. It was most probably some astronomical clustering aswell.
2) I think Hannes explained this pretty exhaustively, I don’t really see the reasoning behind expecting it to be circular if it is a fairly homogenous distribution. A nice analogue might be an axis of symmetry – if the volume/points are divided equally between the two points, then the boundary should just be the axis of reflectionary symmetry, which is a straight line. Corners are just made up from the straight lines of more than two axes.
3) As the number of centres increases, the number of neighbouring centres increases, thus a single centre has a higher number of straight line boundaries which means they go from looking like rectangles/triangles to hexagon, octagons … until they look closer to circles (or just a mesh with a more uniform cell volume and shape).
I think Hannes is right, every point adds a new polygon and also gets area of some of the other polygons. For each taken area, there is a new separating plane represented by a line. To answer the first question, it is called Voronoi diagram.
I think Hannes got it right: the set of points equidistant from two given points is a line orthogonal to the segment connecting the two points. So, adding more points, one should expect the boundaries to be shaped like polygons with an increasing number of sides.
I only have to add that these plots are called Voronoi diagrams.
I think Hannes got it right: the set of points equidistant from two given points is a line orthogonal to the segment connecting the two points. So, adding more points, one should expect the boundaries to be shaped like polygons with an increasing number of sides.
I only have to add that these plots are called Voronoi diagrams. But yeah, most of the quiz was already answered by Hannes 😉
Hannes was right, but the first who answered all questions (Hannes didn’t write the name of diagrams) was Jasper. Congratulations Jasper! You won this quizz.
Thank you for your interest in this quizz, we hope next qiuzzes will come early.
BTW, for those who would like to think about it differently – eventually to cover a rectangular space, one must use some method of triangulation (that’s the basic primitive and no higher/lower order polygon).
Although as the number of partitions will increase it will reach a shape closer to a circle, but never will, because of the way Euclidean space is formed.
So triangles my friends, triangles :).
Even though I don’t get it now: what was the award?
Learning something new.
Plus, there will be an award.
We’ll contact the winners in person for further details :).