A (hopefully) gentle introduction to lattice QCD

As I have mentioned in my previous blog posts, my Summer of HPC project is optimizing software for lattice quantum chromodaynamics computations. Since this probably doesn’t ring a bell for someone who has not studied physics, I will try to provide a gentle introduction to the topic, its applications, the role of high performance computing and why it is so exciting.

So what is lattice QCD? In short, lattice quantum chromodynamics is a computational technique to compute the forces between quarks and gluons. Or more formally, to solve the equations of quantum chromodynamics. In case you are not familiar with subatomic physics, this probably still sounds very cryptic to you, so let’s take a step back.

As physicists currently understand the world, everything around us is made up of fundamental particles that interact in one way or another to form complex structures such as atoms, molecules, planets and everything else around us. The currently most successful model in describing these processes is the so-called standard model of particles physics. The standard model contains 61 fundamental particles. Popular examples you probably have heard of are the electron, the photon, the six quarks, or the Higgs boson. These fundamental particles then come together to form all other known composite particles, such as nucleons or mesons. However to do this, they need a force to bind them together. For this the standard model provides three fundamental interactions: The electromagnetic force, the strong force and the weak force. However, not all particles interact with each other through all interactions. Each interaction has an associated property that makes particles with that property interact with each other. For the electromagnetic force this is the electrical charge, that makes particles of equal charge repel each other and particles of opposite charge attract each other. In analogy to electromagnetism, the corresponding property for the strong force is called color charge.   What we are dealing with in quantum chromodynamics are particles that carry color charge and interact with each other through a strong force. There is actually also a fourth fundamental interaction, gravity, but the theory of the standard model is not able to describe this one properly.

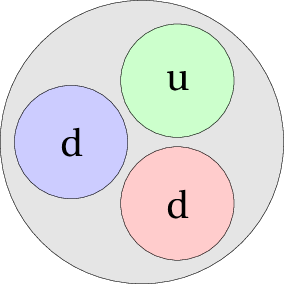
A neutron made up of two down (d) quarks and one up (u) quark. Each of the quark carries color charge red, green or blue. Which quark carries which charge is arbitrary, but all three must be present in a neutron

Now that we have a rough idea about what we are dealing with, let’s get a bit more into detail. As mentioned above, the property that makes particles interact strongly with each other is called color charge. However, instead of just one type of electric charge, there are three color charges: red, green, and blue. Needless to say, they have nothing to do with actual colors, it is just as an analogy to the primary colors of human vision. The fundamental particles that carry color charge are the 6 different quarks and the 8 different gluons. So the particles that interact with each other through the strong force are the quarks, the gluons and particles that are made
up of them, such as the nucleons, mesons . Even though the analogy to electromagnetism worked quite well up to now, the strong force has some very interesting properties that distinguish it from electromagnetism, but going into detail on them would be a bit too much for now. Luckily, the theoretical physicists have done a pretty good job and put everything we need to describe interacting quarks and gluons into one handy formula:

If you think about that this is all you need to describe quarks and gluons interacting with each other,  this looks actually pretty simple, doesn’t it? However, this equation is actually a bit more complicated than it may seem. One reason is that we are not  dealing with normal numbers, but rather with quantum mechanical operators. The other is that there are quite a few things hidden away in the notation. It’s actually so bad, that we cannot obtain an exact solution from this equation. This is where the lattice comes into play. Lattice QCD is a technique to extract approximate, physical quantities from the equations of quantum chromodynamics. The main simplification here is to look for solutions only at a finite number of points in space and time instead of infinitely many. Those points in space and time may be viewed to form a 4-dimensional lattice in  space and time and this is where the method has taken its name from. However, there is quite a bit more involved to get from the above equation to physically meaningful properties, such as for example the mass of the proton, but don’t worry I will not get into any more detail on this.

So if we simplified the whole thing, why do we still need supercomputers for this? The reason is that if we want approximate values that we can expect to be close to the real physical values, we need to make the lattice finer and finer. A typical lattice size is 48 points in each of the three spatial dimensions and 96 points in the time dimension. This might not sound much, but to do describe this lattice we already need vectors with more than 100 million elements, which takes about two gigabytes of memory to store. And of those vectors we need quite a few more and we also need to do computations with them. Believe me, this isn’t something you can do with your computer at home.

At this point you may still ask yourself: So what’s the point in all of this? The point is that physicists are still trying to find out whether the standard model really is an accurate description of the actual world. For this they need to make predictions from the theory that can be validated in experiments. By building a bridge between theoretical physics and the real world, lattice QCD and high performance computing help us advance our understanding of the fundamental processes that make the world around us what it is. If this is not exciting, then I don’t know what is.