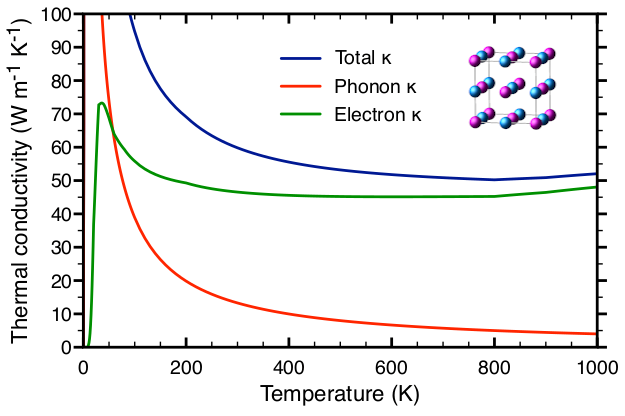
Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2215

Today’s supercomputing hardware provides a tremendous amount of floating point operations (FLOPs). Hierarchical algorithms like the Fast Multipole Method (FMM) can achieve a very good  utilization of the FLOPs coming from a single node. However, modern supercomputer consist of a large number of these powerful nodes and explicit communication is required to drive the computation and increase the scaling further.
Unfortunately, such communication is not a trivial thing, since we are not able to duplicate all data in memory at every node and also do not want to wait for communication longer than absolutely necessary.
In this project we want to look into the costs of communicating via message passing (MPI). Our target application will be the Fast Multipole Method (FMM) and during the project we will scale the application to a large number of compute nodes.
Depending on your interest and prior knowledge, we will pursue different goals. First, we want to have a look at the communication pattern of a simple Coulomb solver and implement a global communication pattern via MPI that does scale better than a naive point-to-point or global communication step. Second, the communication of the full FMM will be considered. Since, the algorithm consists of 5 different passes inside, different communication algorithms are required and can be benchmarked and tested.
The challenge of both assignments is scale to large number of nodes without introducing visible overheads from the communication layer.
What is MPI? MPI stands for message passing interface and is the de facto standard of communication between nodes in HPC. It provides hundreds of different collective communication primitives like broadcast, gather and scatter as well as point-to-point primitives like send, receive, put, and get. Due to its generic interface the user can build his own communication algorithms on top of MPI and thereby optimize the flow of data.
What is the fast multipole method? The FMM is a Coulomb solver and allows to compute long-range forces for molecular dynamics, e.g. GROMACS. A straightforward approach is limited to small particle numbers N due to the O(N^2) scaling. Fast summation methods such as PME, multigrid or the FMM are capable of reducing the algorithmic complexity to O(N log N) or even O(N).  However, each fast summation method has auxiliary parameters, data structures and memory requirements which need to be provided. The layout and implementation of such algorithms on modern hardware strongly depends on the available features of the underlying architecture.

Inside the brain of the 2022 PRACE SoHPC student after two weeks of parallel thinking.

Project Mentor: Ivo Kabadshow

Project Co-mentor: Andreas Beckmann

Site Co-ordinator: Ivo Kabadshow

Learning Outcomes:
The students will learn that node to node communication can be a bottleneck for many algorithms in HPC. Additionally, the students will see how proper communication algorithms can circumvent and avoid the bottleneck and scaling to a large number of nodes can be improved.The students will learn that node to node communication can be a bottleneck for many algorithms in HPC. Additionally, the students will see how proper communication algorithms can circumvent and avoid the bottleneck and scaling to a large number of nodes can be improved.

 Student Prerequisites (compulsory):

Prerequisites

  • Programming knowledge for at least 5 years in C++
  • Basic understanding of message passing
  • “Extra-mile” mentality

Student Prerequisites (desirable):

  • MPI or general node-node communication desirable, but not required
  • C++ template metaprogramming
  • Interest in C++11/14/17 features
  • Interest in performance optimizations
  • Ideally student of computer science, mathematics, but not required
  • Basic knowledge on benchmarking, numerical methods
  • Mild coffee addiction
  • Basic knowledge of git, LaTeX, TikZ

 

Training Materials:
Just send an email … training material strongly depends on your personal level of knowledge. We can provide early access to the  cluster as well as technical reports from former students on the topic. If you feel unsure about the requirements, but do like the project, send an email to the mentor and ask for a small programming exercise.

Workplan:
Week – Work package

  1. Training and introduction to FMMs and message passing
  2. Trivial implementation of parallel Coulomb solver
  3. Advanced implementation of parallel Coulomb solver
  4. First scaling benchmarks and optimizations
  5. Trivial implementation of parallel FMM
  6. Advanced implementation of parallel Coulomb solver
  7. Optimization and benchmarking, documentation
  8. Generating of final performance results. Preparation of plots/figures. Submission of results.

Final Product Description:
The final result will be a node-parallel FMM code via MPI to support scaling to a large number of nodes. The benchmarking results, especially the gain in performance can be easily illustrated in appropriate figures, as is routinely done by PRACE and HPC vendors. Such plots could be used by PRACE.

Adapting the Project: Increasing the Difficulty:
The FMM consists of multiple passes with different levels of parallelization difficulties.  A particularly able student may also implement different strategies and pattern. Depending on the knowledge level, a more detailed dive into MPI (one-sided, group communicators, etc.) can take place to tune the performance further.

Adapting the Project: Decreasing the Difficulty:
Should a student that finds the task of optimizing a complex kernel too challenging, could restrict himself to simple or toy kernels, in order to have a learning experience. Alternatively, if the student finds a particular method too complex for the time available, a less involved algorithm can be selected.

Resources:
As explained above, a student that finds the task of adapting/optimizing the MPI communication layer to all passes too challenging, could very well restrict himself to a simpler model or a subset of FMM passes.

Organisation:
JSC-Jülich Supercomputing Centre

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2214

Simulations of classical or quantum field theories often rely on a lattice discretized version of the underlying theory. For example, simulations of Lattice Quantum Chromodynamics (QCD, the theory of quarks and gluons) are used to study properties of strongly interacting matter and can, e.g., be used to calculate properties of the quark-gluon plasma, a phase of matter that existed a few milliseconds after the Big Bang (at temperatures larger than a trillion degrees Celsius). Such simulations take up a large fraction of the available supercomputing resources worldwide.
Other theories have a lattice structure already “build in”, as is the case for graphene, with its famous honeycomb structure, but other carbon nano-systems such as nanotubes. Simulations studying this material can build on the experience gathered in Lattice QCD. These simulations require, e.g., the repeated computation of solutions of extremely sparse linear systems and update their degrees of freedom using symplectic integrators.
Depending on personal preference, the student can decide to work on carbon nano-systems or on Lattice QCD. He/she will be involved in tuning and scaling the most critical parts of a specific method, or attempt to optimize for a specific architecture in the algorithm space.
In the former case, the student can select among different target architectures, ranging from Intel XeonPhi (KNL), Intel Xeon, AMD EPYC or GPUs (NVIDIA A100), which are available in different installations at the institute. To that end, he/she will benchmark the method and identify the relevant kernels. He/she will analyse the performance of the kernels, identify performance bottlenecks, and develop strategies to solve these – if possible taking similarities between the target architectures (such as SIMD vectors) into account. He/she will optimize the kernels and document the steps taken in the optimization as well as the performance results achieved.
In the latter case, the student will, after getting familiar with the architectures, explore different methods by either implementing them or using those that have already been implemented. He/she will explore how the algorithmic properties match the hardware capabilities. He/she will test the archived total performance, and study bottlenecks e.g. using profiling tools. He/she will then test the method at different scales and document the findings.
In any case, the student is embedded in an extended infrastructure of hardware, computing, and benchmarking experts at the institute.

QCD & HPC

Project Mentor: Prof. Dr. Stefan Krieg

Project Co-mentor: Dr. Eric Gregory

Site Co-ordinator: Ivo Kabadshow

Learning Outcomes:
The student will familiarize himself with important new HPC architectures, such as AMD, Intel, NVIDIA or other accelerated architectures. He/she will learn how the hardware functions on a low level and use this knowledge to devise optimal software and algorithms. He/she will use state-of-the art benchmarking tools to achieve optimal performance.

 Student Prerequisites (compulsory):

  • Programming experience in C/C++

Student Prerequisites (desirable):

  • Knowledge of computer architectures
  • Basic knowledge on numerical methods
  • Basic knowledge on benchmarking
  • Computer science, mathematics, or physics background

Training Materials:

Supercomputers @ JSC
http://www.fz-juelich.de/ias/jsc/EN/Expertise/Supercomputers/supercomputers_node.html

Architectures
https://developer.nvidia.com/cuda-zone
http://www.openacc.org/content/education

Paper on MG with introduction to LQCD from the mathematician’s point of view:
http://arxiv.org/abs/1303.1377

Introductory text for LQCD:
http://arxiv.org/abs/hep-lat/0012005
http://arxiv.org/abs/hep-ph/0205181

Introduction to simulations of graphene:
https://arxiv.org/abs/1403.3620
https://arxiv.org/abs/1511.04918

Workplan:
Week – Work package

  1. Training and introduction
  2. Introduction to architectures
  3. Introductory problems
  4. Introduction to methods
  5. Optimization and benchmarking, documentation
  6. Optimization and benchmarking, documentation
  7. Optimization and benchmarking, documentation

Generation of final performance results. Preparation of plots/figures. Submission of results.

Final Product Description:
The end product will be a student educated in the basics of HPC, optimized methods/algortithms or HPC software.

Adapting the Project: Increasing the Difficulty:
The student can choose to work on a more complicated algorithm or aim to optimize a kernel using more low level (“down to the metal”) techniques.

Adapting the Project: Decreasing the Difficulty:
Should a student that finds the task of optimizing a complex kernel too challenging, could restrict himself to simple or toy kernels, in order to have a learning experience. Alternatively, if the student finds a particular method too complex for the time available, a less involved algorithm can be selected.

Resources:
The student will have his own desk in an open-plan office (12 desks in total) or in a separate office (2-3 desks in total), will get access (and computation time) on the required HPC hardware for the project and have his own workplace with fully equipped workstation for the time of the program. A range of performance and benchmarking tools are available on site and can be used within the project. No further resources are required.

Organisation:
JSC-Jülich Supercomputing Centre

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2213

As the costs of electricity in Europe are rapidly growing, peaking more than 600 EUR per MWh in the end of 2021 and having a 200 EUR per MWh on regular basis, a stable and reliable as well as steady delivering energy source is required. This cannot be easily achieved from renewable energy sources due to their rather low efficiency and not solid reliability. Such requirements can be more easily achieved from the nuclear energy, provided some improvements to nuclear fuels are applied. There is a large potential of usage of the so-called Th-cycle with waste to be secured only in matters of years, maximum of a decade, as a large advantage over existing MOX, or UO2 based fuels that are currently applied. Another advantage is to used fuels that are capable of operating at higher temperature, i.e. with higher efficiency of the heat transfer. Naturally, metallic ones will overcome insulating oxides and therefore the actinide compounds will be of our interest. In this project we  would like to simulate the thermal expansion (safety feature) as well as heat transfer, both quantities related to the lattice dynamics. To understand the limits of the fundamental contributions to the heat transfer in novel, potential nuclear fuels for the generation IV reactors, the large quantum-mechanical calculations can be performed on the largest czech national HPC infrastructure.

The electronic and phonon contributions to thermal conductivity calculated using quantum-mechanical calculations without usage of experimental parameters.

Project Mentor: Dominik Legut

Project Co-mentor: Urszula D. Wdowik

Site Co-ordinator: Karina Pešatová

Learning Outcomes:
Knowledge how to calculate dynamical properties of solids, obtain phonon-dependent thermodynamical quantities, simulate transport phenomena in solids.

Student Prerequisites (compulsory):
unix commands, bash, editors vim or emacs, crystal structures and general knowledge of the solid state physics, see the training material

Student Prerequisites (desirable):
Knowledge of sed, awk, and regular expressions which can simplify partially the postprocessing. The knowledge of python and programming in general will be very large advantage for post-processing and development.

Training Materials:

  1. https://www.geeksforgeeks.org/essential-linuxunix-commands/
  2. – KITTEL, Charles. Úvod do fyziky pevných látek. Praha: Academia, 1985, ISBN-13: 978-0471874744.
  3. – MANES, L. Actinides – Chemistry and Physical Properties. Berlin, Heidelberg: Springer-Verlag, 1985 ISBN 9783540390428.
  4. – MARTIN, R. M., Electronic Structure: Basic Theory and Practical Methods, Cambridge University Press, 2004, ISBN-13: 978-0521782852.
  5. – ASCROFT N. W. and N. D. Mermin, Solid State Physics, Cengage Learning, 1976, ISBN-13: 978-0030839931.
  6. – KAXIRAS, Efthimios. Atomic and electronic structure of solids. New York: Cambridge University Press, 2003. ISBN 978-0521523394.
  7. – CHAIKIN, P. M. and T. C. LUBENSKY. Principles of condensed matter physics. Cam- bridge [u.a.]: Cambridge Univ. Press, 2007. ISBN 9780521794503.
  8. SINGLETON, J., Band Theory and Electronic Properties of Solids, Oxford Master Series in Physics, 2001, ISBN-10: 0198505914.
  9. – BLUNDELL, Stephen. Magnetism in condensed matter. Oxford: Oxford University Press, Oxford master series in condensed matter physics. ISBN 9780198505914.
  10. – GRIMVALL, Göran. Thermophysical properties of materials. Enl. and rev. ed. New York: Elsevier, 1999. ISBN 0444827943.

Workplan:

1w: Introduction to the density funcitional theory calculations.
2w: Performing electronic structure calculations.
3w: Introduction to the calculations of lattice dynamics (phonons).
4w: Analysis of the calculated results – physical quantities to acquire.
5-8w: Performing calculations of phonon-phonon interaction for simple systems.

Final Product Description:
Determination of the leading terms in thermal conductivity for given materials. Finding the limits of the models.

Adapting the Project: Increasing the Difficulty:
To increase complexity of modelling we can involve calculations of electron-phonon interactions.

Adapting the Project: Decreasing the Difficulty:
Omission of the electron-phonon interactions (QuantumEspresso, EPW codes). Application of standard routines of the Phono3py code and limitation of calculations to lattice thermal conductivity.

Resources:
Phonopy, Phono3py, VASP, Quantum Espresso, EPW, all codes are available at IT4Innovations HPC clusters within the supervisor’s group

Organisation:
IT4Innovations National Supercomputing Center at VSB – Technical University of Ostrava

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2212

Quantum computers are based on a completely different principle than classical computers. The aim of this project is to explain this difference. Thanks to this insight, potential students should then understand, for example, why quantum computers are able to solve the problem of exponential complexity in less than exponential time, what is the difference between quantum natural parallelism and parallel programming on HPC, or what the principle of quantum teleportation is based on.
As this field has been undergoing hectic progress in recent times, new research results are constantly being published. It is therefore not possible to cover all of these new developments in a few weeks of teaching, so this project will focus mainly on the theoretical foundations, mathematical description and practical testing of the resulting quantum circuits on real quantum computers and their simulators.

Project Mentor: Jiří Tomčala

Project Co-mentor: /

Site Co-ordinator: Karina Pešatová

Learning Outcomes:
Students should be introduced to a completely different principle of quantum computers and their programming. They should also be able to design basic quantum circuits.

Student Prerequisites (compulsory):
Knowledge of basic linear algebra.

Student Prerequisites (desirable):
Imagination and experience with Python programming.

Training Materials:
“Quantum Computation and Quantum Information” by Isaac Chuang and Michael Nielsen.
“Quantum Algorithm Implementations for Beginners” by various authors, which can be downloaded from here: https://arxiv.org/pdf/1804.03719.pdf
Etc.

Workplan:

1st week: Quantum bits
2nd week: Single qubit operations
3rd week: Quantum gates
4th week: Quantum teleportation
5th week: Deutsch–Jozsa algorithm
6th week: Grover’s algorithm
7th week: Quantum Fourier transform
8th week: Shor’s algorithm

Final Product Description:
Students test their own quantum circuits on a simulator and, if possible, on a real quantum computer. This includes the correct evaluation of their measured results.

Adapting the Project: Increasing the Difficulty:
Attempting to create interesting modifications of the discussed algorithms.

Adapting the Project: Decreasing the Difficulty:
Skipping overly complicated algorithms.

Resources:

Organisation:
IT4Innovations National Supercomputing Center at VSB – Technical University of Ostrava

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2211

Space is a harsh environment; however, it is not totally void. In the solar system, space is filled with charged particles continuously expelled from the Sun corona. This flow is the so-called “solar wind”. Our goal is to deepen the understanding of the mechanisms at play in the interaction between such solar wind and the planets of the solar system.

Our group addresses the study of this interaction via three-dimensional, full-kinetic plasma simulations. To put it in a nutshell, our simulation code solves the Maxwell equations for the electromagnetic fields coupled with the equation of motion for the solar wind particles (forming a so called “collisionless plasma”). Such nonlinear coupling is at the origin of the complex and intricate behavior governing such systems. Eventually, we aim at comparing the results of our simulations with spacecraft observations around planets of the solar system. Our work therefore directly supports solar system exploration and in situ observations performed by several space missions from ESA (European Space Agency) and JAXA (Japanese Space Agency) such as the exploratory planetary missions Rosetta, BepiColombo, Juice.

With our HPC numerical simulations, typical running on Tier-1 and Tier-0 computing centers, we can model Sun-Planet interaction but at the cost of producing large dataset of physical quantities around the planet (including electric and magnetic fields, particles trajectories etc). These outputs need careful and efficient post-processing. Such post-processing based on HPDA approach is the goal of this student research project.

This HPDA project focuses on increasing the efficiency and reliability of our post-processing techniques. Given the raw simulation outputs, the tasks for this project concern the computation of (1) velocity distribution function for particles, (2) particle currents and fluxes onto the planet surface, (3) global 3D shape of the planetary magnetic field. The accomplishment of this tasks will enable a much more efficient analysis of the simulation, and thus a much higher scientific impact. To conclude, the goal of this project is to build – from a given set of simulations output – efficient and scientifically rigorous post-processing routines that would eventually run in parallel on the computer center where the HPC simulations are performed.

Outline of the post-processing pipeline at the basis of this project. From left to right:
(left panel) we obtain the raw simulation data from our code, stored at the HPC center,
(Middle panel) these data are first processed at the HPC center to visualize them and understand the overall dynamics in the simulation. In the middle panel, we show a 2D cut of the electron current around the planet, the solar wind is flowing from left to right and the planet is shown by a gray solid sphere in the center of the box,
(Right panel) in a second, more refined, post-processing level we address in detail a specific physical process of interest, as an example in the right panel we show a comparison between electron energy distribution functions both from the simulation (upper panel) and from the Mariner10 spacecraft in-situ data at Mercury (bottom panel).

Project Mentor: Pierre Henri

Project Co-mentor: Federico Lavorenti

Site Co-ordinator: Karim Hasnaoui

Learning Outcomes:
Development of HPDA skills for scientific research. Get to know the HPC methods used for numerical modeling of space science phenomena and contribute to the interpretation of spacecraft observations.

Student Prerequisites (compulsory):
Background in physics, especially fluid-mechanics and electromagnetism. Coding experience with common scientific computing language (C/C++ and/or Fortran). Familiar with Linux environment.

Student Prerequisites (desirable):
Coding experience with Python.
Parallel coding (MPI and/or OpenMP).
Plasma physics.

Training Materials:
Some video of our simulations: https://vimeo.com/user146522309
The simulation code: https://github.com/KTH-HPC/iPIC3D
A scientific article explaining the code: https://doi.org/10.1016/j.matcom.2009.08.038
A scientific article showing an application of this code: https://doi.org/10.1103/PhysRevLett.123.055101

Workplan:
The workplan is organized as follows:

  1. Training week (W1)
  2. Introduction to the working environment, the workflow of the simulation code, the structure of the code output, and the existing post-processing routines (W3)
  3. Definition of the most suitable approach to optimize the existing routines and implement the new ones (W3)
  4. Optimization and implementation (W4-W5)
  5. Validation and debugging (W6-W7)
  6. Final report writing (W8)

Final Product Description:

– Optimization of the existing post-processing routines (currently written in python in serial) for both 1st and 2nd level analysis, to be parallelized and to eventually run on the HPC center where the dataset is stored.
– Implementation of new post-processing routines (parallel and to eventually run on the HPC center where the dataset is stored) to extend the 2nd level scientific analysis.

Adapting the Project: Increasing the Difficulty:
The implementation of the new routines could be implemented directly within in the simulator code structure, in order to perform the post-processing directly during the HPC run, instead of post-processing the simulation output.

Adapting the Project: Decreasing the Difficulty:
Focus only on the optimization of the existing routines.

Resources:

  • Datasets from HPC simulations will be provided
  • The simulator will be provided
  • No s/w license will be necessary
  • To avoid foreseen difficulties regarding the access to Tier-0 facilities for summer students, we will use a Tier-2 center instead on which the HPC output data will be transferred. The « Maison de la Simulation » has agreed to give to both the students and the tutors access to the Paris-Saclay mesocenter (http://mesocentre.centralesupelec.fr/) during the duration of the project.
  • NB: Computer not provided if online project

Organisation:
IDRIS, Laboratoire Lagrange, Observatoire de la Côte d’Azur, Université Côte d’Azur, CNRS, Nice, France

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2210

Direct numerical simulations of turbulence flows are still challenging and need the performance of the fastest super-computers in the world. As the latter are nowadays of heterogeneous architecture, i.e. mixing CPUs and accelerators such as GPUs, algorithms updated. In this project we will explore the benefits of the new programming languages (SYCL and/or Kokkos) for turbulence simulations. SYCL is a high-level programming standard for heterogeneous computing.  It is a single code language (one file for CPU and GPUs) and closely tied to modern C++. Kokkos is library with a usage similar to SYCL. More precisely, this project aims at porting an existing high-order Discontinuous Galerkin (DG) C++ code to CPU-GPU computers in order to challenge well establish CPU codes. The DG code solves partial differential equations, such as shallow water or Navier-Stokes, from fluid mechanics in Cartesian coordinates as well as on the sphere. The latter coordinates use an interesting map called “cubed sphere” borrowed from differential geometry.

Deformational flow on the two-dimensional sphere surface

Project Mentor: Holger Homann

Project Co-mentor: /

Site Co-ordinator: Karim Hasnaoui

Learning Outcomes:
Students will be in touch with modern fluid dynamical algorithms (Discontinuous Galerkin), modern C++ (SYCL and/or Kokkos), and advanced mathematics (partial differential equations and differential geometry)

Student Prerequisites (compulsory):

– Excellent C++ programming skills
– Knowledge on numerical methods for fluid dynamics

Student Prerequisites (desirable):

– Knowledge on CUDA or OPENCL or MPI or OPENMP

Training Materials:

– Excellent tutorial: “Emerging numerical methods for atmospheric modeling” by Nair, R. D., Levy, M. N., & Lauritzen, P. H. (2010) https://opensky.ucar.edu/islandora/object/books%3A214
– Tutorial on SYCL with online coding and testing: https://www.codingame.com/playgrounds/48226/introduction-to-sycl/introduction-to-sycl-2
– Video + hands on Kokkos https://www.youtube.com/watch?v=PjWwith05oA

Workplan:

1-2 week: training and tests of porting a simple 1D Discontinuous Galerkin code with SYCL
3-7 week: Porting of the scientific production code to SYCL/Kokkos

SYCL and Kokkos being a programming languages under heavy development, finding and adapting the best data layout is not trivial. The existing DG code uses modern C++ abstractions. Porting these to SYCL and/or Kokkos is a challenging task that surely benefits form discussion among 2 or 3 students. Various tests of simplified codelets will certainly be usefull.

Final Product Description:
Performance comparison of pure C++ and SYCL/Kokkos implementations of a discontinuous Galerkin solver.

Adapting the Project: Increasing the Difficulty:
The code is made up of different unities that need, such as the spherical geometry in terms of the “cubed sphere” map. Starting from the basics routines, students can study more complex parts of the code.

Adapting the Project: Decreasing the Difficulty:
Only example parts of the code can be tested with SYCL and/or Kokkos and benchmarked to get an idea of the performance of the whole code.

Resources:

– Recent SYCL compiler – such as Intel’s dpcpp
– Kokkos environment
– Modern GPGPU server

Test systems are available in the host institute. A test account on the Idris machine Jean Zay would be beneficial.

Organisation:
IDRIS, OCA-Laboratoire Lagrange UMR7293, Observatoire de la Côte d’Azur

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2209

The numerical simulation of wave propagation phenomena is of great interest in many areas of science and engineering, including seismic and acoustic applications. In this context, the use of time-domain solvers enables to significantly reduce the memory requirements and the need to devise effective preconditioners, when compared to frequency domain solvers. The efficiency of a time-domain simulation using explicit time marching algorithms is directly linked to the stability limit of the selected time marching scheme (i.e. the time stepΔt), especially for long simulations: the larger Δt assuring stability, the lower the number of iterations required. In the Spectral Element Method (SEM, a finite element method with high-order polynomials) the classical stability condition (i.e. the Courant Friedrichs Lewy condition, CFL) depends on the polynomial order and it can be estimated for homogeneous domains and structured mesh only. The CFL condition reads:

α=c Δt / h ⩽αm

with c being the wave speed andhthe characteristic element size.
Previous analyses revealed instabilities are often observed when the CFL stability limit derived for homogeneous materials is adapted to heterogeneous media by simply using the lowest local velocity. This inconvenient leads to apply arbitrary safety factor to αm, ending up in extremely small Δt(~10-6 s).

The objective of this work is to implement an advanced stability criterion that is accurate for heterogeneous elastic and acoustic media, in a HPC wave propagation solver based on the spectral element method, called SEM3D. The latter is an efficient HPC software, based on a spatial domain decomposition scheme for parallel distributed-memory resolution and it includes a large-scale random field generator to add randomly distributed heterogeneity to the problem at stake. SEM3D runs in production phase and it has been widely tested on several supercomputers and on 10000+ CPU cores.

The internship will be focused on implementing an element-wise stability criterion in SEM3D, that accounts for the local material heterogeneity (non-periodic) but that conditions the whole simulation. This challenging task resorts to solve as fast as possible several element-wise eigenvalue problems on each domain partition, without assembling the local mass and stiffness matrices. Advanced algebraic libraries will be employed. Based on the advancements, the work can be extended to the implementation of an element-wise time-marching scheme with different time-stepping (and accuracy) based on the local stability condition.

The development and testing phase will be done on the Mésocentre Moulon supercomputer facilities, where SEM3D is already compiled.

Computing a local stability condition for heterogeneous elastoacoustic problems, in a domain decomposition parallel scheme.

Project Mentor: Filippo Gatti

Project Co-mentor: Régis Cottereau

Site Co-ordinator: Karim Hasnaoui

Learning Outcomes:
The intern(s) will be learning how the spectral element method is implemented in a modern HPC environment, as well as to implement an advanced stability condition by solving an eigenvalue problem via advanced parallel schemes.

Student Prerequisites (compulsory):

Student of Engineering or Physic

  •  Background on the Finite Element Method and applied math
  •  Basics in coding for scientific applications

Student Prerequisites (desirable):

  • MPI/OpenMP
  •  fortran90/C++

Training Materials:
https://onlinelibrary.w iley.com/doi/abs/10.1002/nme.5922
https://igpppublic.ucsd.edu/~shearer/227C/spec_elem_monograph.pdf

Workplan:

  • Week 1: Training on SEM3D (including automated non-regression testing) + literature review
  • Week 2: feasibility study, testing available libraries for eigenvalue problem resolution to be linked to SEM3D
  • Week 3: Plan redaction and submission, construction of a suite of case studies
  •  Week 4-6: Implementation of stability condition for acoustic problems (student 1) and for elastic problems (student 2)
  •  Weeks 7: Extensive test on the defined case studies and on automated non-regression test cases
  • Week 8: Final Report editing and submission

Final Product Description:
At the end of project, SEM3D is expected to be running on extremely large and heterogeneous elastoacoustic set-ups with the largest time step possible, according to the element-wise stability criterion computed beforehand.

Adapting the Project: Increasing the Difficulty:
Implement different time-marching schemes depending on the stability

Adapting the Project: Decreasing the Difficulty:
Implement the element-wise stability condition on acoustic problems only.

Resources:
The project is entirely based on SEM3D, which is proprietary code and that will be delivered to the student. The project will be conducted by exploiting the computational resources of the Mésocentre Moulon (http://mesocentre.centralesupelec.fr/), the pool of supercomputer resources of CentraleSupélec and ENS ParisSaclay. An account will be assigned to the student by the time the project starts. Student(s) will connect remotely via ssh to the supercomputer facility, with no limitation (within the common user’s policy).

SEM3D is already compiled and it has been extensively tested on the Mésocentre Moulon supercomputer facilities, which include dedicated nodes for visualization and post-processing.

Organisation:
IDRIS, CentraleSupelec

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2208

Neural networks have shown remarkable performance in lots of domains to solve problems of high complexity. They can, in principle, be used to learn any type of model as they are universal approximators. Their use would be of a great benefit as they can be intended to automate major tasks within an engineering project (such as structural sizing, dimensioning certification, criteria verification, …). However, it is not yet usual to use these technics; may be for lack of competitiveness against feedforward calculations. One major issue is the robustness and the difficulty to ensure high precisions for deterministic predictions.
In this project, we would like to investigate the ability of neural networks to approximate mechanical models and their performance in terms of precision. Increasing accuracy requires understanding how these models work in a deeper way.
Datasets from several models of different complexities will be provided to train neural networks and study their performance and robustness. The type of problems we are dealing with use, conveniently, metrics in terms of relative error. Such metric may yield poor accuracy, especially for target values of low amplitudes.
As a first approach to improve a neural network performance, all needed resources can be used to evaluate the maximum achievable precision. A theoretical reflexion can then be done to understand the unsurmountable limiting factors (numerical precision, model architecture, type of the model, nonlinear behaviour, size of the dataset, …).
After the justification of the limitations, a second step would be to optimize the capacity of the used models in a way to reduce the computational costs whilst maintaining the same level of performance.

Influence of the architecture and nonlinear features on the performance of a neural network.

Project Mentor: Yassine EL ASSAMI

Project Co-mentor: Benoit Gely

Site Co-ordinator: Karim Hasnaoui

Learning Outcomes:
This project will allow the students to understand the functioning of neural networks and practice with high performance computational resources.

Student Prerequisites (compulsory):
This work is relevant for a student with a scientific profile with competence in computational science and machine learning.

Student Prerequisites (desirable):
A knowledge of the mechanical engineering domain is a plus. It is also desirable to have some ease with theoretical mathematics.

Training Materials:
Any course in the field of machine learning could be interesting.
We advise “Fidle project” (for French speakers).
Sites like Coursera, Kaggle and HuggingFace are also good references.

Workplan:
In this project, several data and scripts may be provided for starting.

  • 1 week is expected to make some bibliography search about the subject.
  • 2 to 3 weeks are needed to study precision enhancement: test different architectures, optimize hyperparameters, make cluster computations for fine tuning.
  • 1 week would be needed for theoretical reflexions.
  • 1 week to try model optimization to reduce computational cost.

Final Product Description:
The students will implement calculations that should be well documented and conveniently structured to meet scientific required quality. Also, a scientific report about this work is to be provided.

Adapting the Project: Increasing the Difficulty:
We intend to work mostly with dense layers. But other types of architectures may be used if justified in terms of precision (like model stacking or even adversarial networks).

Adapting the Project: Decreasing the Difficulty:
Some provided data is based on very simplified problems that would allow a better understanding of the weights. It is also possible to make studies for specific parameters and study how they affect performance.

Resources:
The students would mostly work with machine learning libraries (Sklearn, Tensorflow) on Python. The use of Git is advised to exchange scripts with the mentors. The resources of the Paris-Saclay mesocentre can be allocated for the duration of the internship [http://mesocentre.centralesupelec.fr/]

Organisation:
IDRIS, Capgemini Engineering – Technology & Engineering Center (TEC)

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2207

Permafrost modeling is important for climate change impacts assessment both in cold areas (especially intensive warming occurring there) and globally (massive quantities of frozen organic C stored in the near surface permafrost). It has also numerous applications in civil and environmental engineering (artificial ground freezing, infrastructure stabilities and water supply in cold regions, …). It requires High Performance Computing techniques because of the numerous non-linearities and couplings encountered in the underlying physics (thermo-hydrological transfers in soil with freeze/thaw). For instance, permaFoam, the OpenFOAM® (openfoam.com, openfoam.org) solver for permafrost modeling, has been used intensively with 500 cores working in parallel for studying a permafrost dominated watershed in Central Siberia, the Kulingdakan watershed (Orgogozo et al., Permafrost and Periglacial Processes 2019), and tested for parallel computing capabilities up to 4000 cores (e.g.: Orgogozo et al., InterPore 2020). Due to the large scales to be dealt with in the HiPerBorea project (3D modelling for tens of square kilometers, century time scale – hiperborea.omp.eu), it is anticipated that the use of permaFoam with at least tens of thousands of cores simultaneously will be needed on one billion cells mesh. This internship aims at characterizing the scalability behaviour of permaFoam in this range of number of parallel computing tasks, and giving a first insight in the code profile using appropriate profiler. A try on new architectures (Fujitsu-like processors) will also be performed. A 3D OpenFOAM® case which simulates the permafrost dynamics in the Kulingdakan watershed under current climatic conditions (Xavier et al., in prep) will be used as a test cases for this study. The used supercomputing infrastructures will be Occigen (CINES) and Irene-ROME (TGCC).

Overview of the HiPerBorea project as presented at the OpenFOAM® Conference held in Berlin in October 2019.

Pre-existing characterization of scalabilty of permaFoam on different supercomputers, different mesh size used.

Project Mentor: Orgogozo Laurent

Project Co-mentor: Xavier Thibault

Site Co-ordinator: Karim Hasnaoui

Learning Outcomes:
The first outcomes for the student will be to get used with the well known, open source, high performance computing friendly CFD toolbox OpenFOAM. The student will also get familiar with the basics of massively parallel computing on supercomputers of today.

Student Prerequisites (compulsory):
Programming skills, basic knowledge of LINUX environment, dynamism, and sense of initiative.

Student Prerequisites (desirable):
C/C++/Bash/Python programming skills.
First experience with OpenFOAM.
Interest for environmental issues and climate change.

Training Materials:
OpenFOAM: https://www.openfoam.com/
Paraview: https://www.paraview.org/
Project HiPerBorea website: https://hiperborea.omp.eu

Workplan:

Week 1: Training week
Week 2-3: Bibliography, OpenFOAM tutorials, first simulations on supercomputer.
Week 4-5: Design and perform scalability study, code profiling, performance analysis on different supercomputers
Week 6-7: Complete simulation on under research watershed, postprocessing and analysis
Week 8: Report completion and presentation preparation.

Final Product Description:
The main deliverable of the project will be a set of  performance analysis with permaFoam for contrasted physical conditions and on different supercomputing systems (Occigen, Irene).

Adapting the Project: Increasing the Difficulty:
If the candidate is at ease in supercomputing environment, extension of the scalability study and code profiling can be performed.

Adapting the Project: Decreasing the Difficulty:
“Realistic” simulations planned for week 6-7 can be discarded to focus on computational topic.

Resources:
PermaFoam solver, accounts on the DARI project A0060110794 for Occigen (CINES) and Irene (TGCC), on both of which OpenFOAM is installed as a default computational tool, Input data to be delivered by L. Orgogozo and T. Xavier.

Organisation:
IDRIS, GET-Geosciences Environment Toulouse

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2206

The Julia language is one of the most modern and effective languages for performing high-performance numerical simulations, particularly in fluid mechanics. This project involves implementing a 2D Julia code simulating the transport of a scalar function with a steep front. The speed of propagation will be calculated as the gradient of a pressure, itself the solution of a Poisson problem that is calculated via the resolution of a linear system. One finds this type of process both in problems of fluid flows in porous media and in problems of propagation of discharges in cold plasmas. The mesh used will be dynamically adaptive and will follow the propagation front according to algorithms previously used with other languages. The goal here is to implement a parallel code at the level of the different calculation phases: first for the dynamic mesh refinement and de-refinement process, then for the resolution of the linear system by direct or iterative methods, and finally for the numerical scheme for calculating the propagation front. In the same way, one must parallelize the method of resolution of the linear system so that each sub-domain is treated by a given number of processes. Knowing that the number and size of the sub-domains vary dynamically during the resolution of the propagation phenomenon. We will proceed step by step. The challenges will be addressed one by one depending on the speed of implementation of the project.

Figure: 3D Streamer propagation using HPC

Project Mentor: Fayssal Benkhaldoun

Project Co-mentor: Mohamed Boubekeur

Site Co-ordinator: Karim Hasnaoui

Learning Outcomes:
The student involved in the project will gain an advanced knowledge of computer code parallelization methods. In addition the student will learn the new lanage Julia which is promising in the context.

Student Prerequisites (compulsory):
In order to carry out the proposed research, the student must necessarily have a good knowledge of methods of approximation of PDEs and methods of solving linear systems.

Student Prerequisites (desirable):
In order to carry out the proposed research, the student will preferably have a Master’s degree in HPC, or have taken advanced courses in this field.

Training Materials:
In order to prepare for the work, the student will be able to consult the Discord workspaces of previous students who have started the project and which contain the codes and reports of the students.

Workplan:

After the training week, the work plan will be as follows, with
algorithms provided:
Week 2: familiarization with the Julia codes already available at the Lab
and bibliographic study concerning the methods of resolution and
parallelization of this type of problem.
Week 3: a work plan will be drawn up based on the study done
previously.
Week 4 A dynamic mesh refinement methodology will be implemented
in the 2D transport resolution code provided to the student.
Week 5 implementation of a parallel method for the direct resolution of
linear systems.
Week 6 implementation of a domain decomposition method based on
adapted non-uniform meshes.
Week 7: Parallelization of the numerical scheme of the calculation of
the transport problem and coupling with the resolution of the linear

Final Product Description:
The project will allow the construction of the skeleton of a Julia platform for calculating fluid flow problems. This will then make it possible to deal with problems that require a lot of CPU time, such as phenomena relating to non-Newtonian fluids.

Adapting the Project: Increasing the Difficulty:
If the situation allows it, we will increase the difficulty by adding the parallization of resolution of linear systems by iterative methods in the 3D framework.

Adapting the Project: Decreasing the Difficulty:
If necessary, we will reduce my difficulty of the project by implementing a parallel code on a very fine but not adapted fixed mesh.

Resources:
The student will have access to and use the Paris 13 University cluster, which has several thousand of computing cores.

Organisation:
IDRIS, LAGA-USPN: Laboratoire Analyse Géométrie t Applications – Université Sorbonne Paris Nord – Paris 13

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2205

Jobs are the essence of the supercomputing. Users creates jobs to solve their scientific and societal challenges, the supercomputing machine executes the job to obtain the aimed results. Crafting efficient jobs which maximises the performance (or minimise the energy efficiency) of the underlying supercomputer HW is a daunting task for the user. Run-time libraries have been developed to turn computational inefficiencies into energy-saving – to reduce the data centre’s carbon footprint. It is thus important to make the user aware of the computational inefficiencies and the energy savings achievable by enabling energy-saving mechanisms in his job run.
This project aims to design a live dashboard of jobs execution, providing to the user and the system administrator with run-time information on the use of microarchitectural components, communication primitives, and computation unbalance.
The Job live dashboard will be built on top of Countdown and Examon frameworks. The first is an MPI energy-saving run-time library deployed at CINECA; the second is a big-data monitoring framework deployed at CINECA to live to monitor the status of the supercomputer. Dashboards will be created using Grafana.

Project Mentor: Andrea Bartolini

Project Co-mentor: Martin Molan

Site Co-ordinator: Massimiliano Guarrasi

Learning Outcomes:
Increase student’s skills in modelling, understanding and visualising the computational characteristics of scientific application.

Student Prerequisites (compulsory):
Computer architecture, basic knowledge of parallel computing.

Student Prerequisites (desirable):
MPI, python, json, previous experience on visualizing data. 

Training Materials:
https://www.youtube.com/watch?v=5ofvPKBzU40

Workplan:

Week 1: Common Training session
Week 2: Introduction to CINECA systems, small tutorials on big data, data collection systems, countdown reporting and detailed work planning.
Week 3: Study of the countdown reported information and Grafana dashboards.
Week 4, 5: Design and testing of the Grafana Dashboard for Jobs.
Week 6, 7: Final stage of the production phase. Implementation of feedback from domain experts and end-users (CINECA staff).
Week 8: Finishing the final movie. Write the final Report.

Final Product Description:
A live dashboard of computational and energy efficiency of jobs in production.

Adapting the Project: Increasing the Difficulty:
Developed advanced performance metrics based on the elaboration of the Countdown data. Development of more complex visualisations.

Adapting the Project: Decreasing the Difficulty:
Design basic visualisation.

Resources:
The student will have access to our facility, our HPC systems and databases monitoring data and the Grafana frontend. The student will be provided with scientific applications and computational hours to collect, analyse the jobs information and design the dashboard.

Organisation:
CINECA – Consorzio Interuniversitario

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2204

The aim of the project is to start the development of methodologies to analyse COPERNICUS satellite data to extract low-resolution bathymetric data in shallow coastal areas where multibeam echosounder data is lacking. These satellite bathymetric extrapolations will provide new information useful for identifying the most critical areas where to plan new high-resolution data acquisitions from Autonomous Underwater Vehicle (AUV) and LiDAR from aircraft.
The challenge will be to develop a method able to extract bathymetry data using Machine Learning from multi-temporal satellite images. Particular emphasis will be placed on the use of HPC resources and the application of Image recognition algorithms related to artificial intelligence such as the Mask Recursive Convolutional Neural Network (Mask R-CNN). The preferred development environment in this case will be Python and the pandas, numpy, keras and tensorflow software packages. For the satellite derived bathymetry, Sentinel-2 or Landsat images along with a large datasets of existing high-resolution bathymetric data will be used.

This picture shows the Ionian Calabrian continental margin ( Ceramicola et al 2014). The colour layer (red to blue) is the bathymetric data acquired during the MAGIC project funded by the Department of Civil Protection to allow the realisation of the first maps of geohazards of the Italian continental margins. In legend are indicated the different geohazard features mapped by an interpreter.

Project Mentor: Silvia Ceramicola

Project Co-mentor: Veerle Huvenne, Gianluca Volpe

Site Co-ordinator: Massimiliano Guarrasi

Learning Outcomes:
The selected student will learn to manage oceanographic and satellite data to integrate different resolution data.
Increase student’s skills about:
– PYTHON
– AI libs (e.g. PyTorch, Keras, TensorFlow, …)

Student Prerequisites (compulsory):
The student will need to have the following compulsory skills:

  • Python
  • Python main scientific libraries (at least basic knowledge):
    • Numpy
    • Pandas
    • Matplotlib
    • …
  • At least one of the following packages:
    • PyTorch
    • Tensorflow, Keras

Student Prerequisites (desirable):
Experience in image recognition methods, GIS

Training Materials:
None

Workplan:

Week 1: Training week with the other SoHPC students
Week 2: Training by CINECA (HPC facility, slurm batch scheduler, VNC, Blender, …) and OGS staff (How to read the data, how to visualize and explore them)
Week 3: Setup the workplan and start the work according with the student abilities and interest
Week 3 (end): Workplan ready.
Week 4-6: Continue the work on structures recognition
Week 7-8: Prepare the final video and report
Week 8 (end): The final video and report will be submitted

Final Product Description:
Our final result will be an automated tool to recognize seabed structures form oceanographic and satellite data. These satellite bathymetric extrapolations will provide new information useful for identifying the most critical areas where to plan new high-resolution data acquisitions from AUV and LiDAR from aircraft. The selected student will also prepare a short video and a final report illustrating his/her work.

Adapting the Project: Increasing the Difficulty:
Depending on the student skills he/she can try to recognize many different type of structures.

Adapting the Project: Decreasing the Difficulty:
In the case the student will not be able to complete the desired tool, he/she will work on the visualization of the data using some visualization tools

Resources:
The oceanographic data and the standard software to inspect them will be given by OGS. Satellite data were taken from Copernicus website (https://www.copernicus.eu/en/copernicus-satellite-data-access). All the needed HPC software (mainly Python, Pytorch, Keras, Fensorflow, Pandas, numpy) is released open source and already available on the CINECA clusters that will be used by the students with their own provided accounts.

Organisation:
CINECA – Consorzio Interuniversitario

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2203

Neural networks (NN) and deep learning are two success stories in modern artificial intelligence. They have led to major advances in image recognition, automatic text generation, and even in self-driving cars. NNs are designed to model the way in which the brain performs tasks or functions of interest. NNs can perform complex computations with ease.
Computational chemistry provides powerful tools for investigation of molecular properties and their reactions. Rapid development of HPC has paved the road for chemists to utilize computational chemistry in their everyday work, i.e. to understand, model, and predict molecular properties and their reactions, properties of materials at nano scale, and reactions and processes taking place in biological systems.
How can we transform the structure of molecules into a form that neural networks understand? In this project, we want to replace the computationally expensive “docking” of molecules into the cavity of a target protein by machine learning and neural network methods. The target protein under study is 3CLpro SARS-CoV-2 (6WQF), which plays a key role in SARS-CoV-2 virus replication. How successful are these methods in preselecting large drug databases to select potential drugs for COVID-19?
This will be achieved by using several available molecular descriptors to account for correlation between structures (i.e. atomic positions) of chemical compounds under investigation and docking score from external computational sources. NNs will be implemented using widely adopted TensorFlow library in Python. For generation of molecular descriptors of chemical systems, we apply DScribe library [1], which can be incorporated as a module directly in Python code. Next to the aforementioned “application part” of the project, we also plan to (in)validate the widely accepted fact, that GPGPUs are superior execution platform for NNs to CPUs.
[1] L. Himanen, M.O.J. Jäger, E.V. Morooka et al., DScribe: Library of descriptors for machine learning in materials science, Computer Physics Communications (2019)

Illustration of 3CLpro SARS-CoV-2 (6WQF) protein, responsible for proteolysis of new virions, represent vital inhibition targets for the COVID19 treatment.

Project Mentor: Ing. Marián Gall, PhD.

Project Co-mentor: Doc. Mgr. Michal Pitoňák, PhD.

Site Co-ordinator: Mgr. Lukáš Demovič, PhD.

Learning Outcomes:
Student will learn about Neural Networks, molecular descriptors, TensorFlow, GPUs and HPC in general.

Student Prerequisites (compulsory):
Basic knowledge of Python and elementary chemistry/physics background.

Student Prerequisites (desirable):
Advanced knowledge of Python, TensorFlow and Keras libraries and other HPC tools. Basic knowledge neural networks and quantum chemistry background.

Training Materials:
https://www.tensorflow.org/
https://singroup.github.io/dscribe/latest/

Workplan:

Week 1: training;
Weeks 2-3: introduction to neural networks, TensorFlow, molecular descriptors, quantum chemistry and efficient implementation of algorithms;
Weeks 4-7: implementation, optimization, and extensive testing/benchmarking of the codes;
Week 8: report completion and presentation preparation

Final Product Description:
Expected project result is Python implementation of (selected) neural network algorithm, applied to quantum chemistry problem. Parallel code will be benchmarked and compared to GPU implementation.

Adapting the Project: Increasing the Difficulty:
Writing own NN algorithm using Python and TensorFlow or build own molecular descriptor for molecular characterization.

Adapting the Project: Decreasing the Difficulty:
Applying existent NN implementation to quantum chemistry problems.

Resources:
Student will have access to the necessary learning material, as well as to our local x86 / GPU Infiniband clusters. The software stack we plan to use is open source.

Organisation:
CC SAS-Computing Centre, Centre of Operations of the Slovak Academy of Sciences

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2202

Nuclear fusion is one of the most promising methods for generating large-scale sustainable and carbon-free energy. Since the 19th century, the rapid rise of global energy consumption and the cumulative CO2 emissions from burning fossil fuels have played a critical role in climate change. Mitigating the harmful effects of climate change is one of the most important challenges for humankind today, which motivates our search for clean energy sources. Fusion is the process that takes place in the sun and generates enormous quantities of heat and light. Therefore, creating a power plant that runs on fusion energy is a very exciting prospect that requires long-term research and development.

Since the 1950s, researchers have tried to replicate nuclear fusion on Earth, a process coined as “building the sun in a box.” However, the conditions in a fusion reactor need to be extremely harsh, with plasma temperatures of over 100 million °C, so that the hydrogen isotopes inside can fuse together and release energy. No design yet has achieved positive net energy gain (more energy generated than used to run the machine), making the optimization and improvement of all components of planned fusion reactors an open question.

In this project, we will use classical molecular dynamics simulations to study the fundamental properties of metals at the atomic scale.  Prior work by Summer of HPC 2021 students in this area will be continued and extended (http://fusion.bsc.es/index.php/2021/08/31/two-students-on-their-internship-in-the-fusion-group/). This line of investigation will help find suitable materials with desirable chemical and physical properties for use as protective layers within fusion reactor walls. Predicting the behaviour of candidate materials as they undergo damage from being near the burning plasma enables engineers to make reactor components that will last longer before needing to be replaced. Such improvements contribute to the goal of feasible industrial power plants by reducing maintenance costs. In examples like this, where experimental data are not available or difficult to obtain, computer simulations are critically important. Furthermore, the continual development of increasingly powerful computers makes discoveries in materials science more achievable than ever before. The outcomes from this study will be key for the continued development of more resistant materials to be used in fusion technologies.

Two examples of atomic-scale damage in tungsten under simulated fusion reactor conditions: an empty bubble (top), and a cascade (right).
These models were produced by Paolo Settembri and Eoin Kearney, SoHPC 2021 fellows at our BSC Fusion Group. View from inside the MareNostrum-4 supercomputer (background).

Project Mentor: Julio Gutiérrez Moreno

Project Co-mentor : Mary Kate Chessey, Mervi Johanna Mantsinen

Site Co-ordinator: Toni Gabaldón

Learning Outcomes:
The student will learn how to model and simulate materials at the atomic scale, using state-of-the-art simulation methods in one of Europe’s largest HPC platforms. The student will gain training and experience in a nuclear fusion research project. .

 Student Prerequisites (compulsory):
Background in Materials Science, Materials Engineering, Physics, Solid State Physics, Theoretical Chemistry, or Computational Chemistry.
Enthusiasm and willingness to learn from mistakes.

Student Prerequisites (desirable):
Organization and communication skills for productive research meetings.
Previous experience with materials simulations from density functional theory or molecular dynamics.
Familiarity with Linux.

Training Materials:
http://fusion.bsc.es/
http://fusion.bsc.es/index.php/2021/08/31/two-students-on-their-internship-in-the-fusion-group/
https://fusionforenergy.europa.eu/
https://lammps.sandia.gov/tutorials.html

Workplan:
The candidate will be part of the BSC Fusion group where they will work in close contact with the group members and the supervisor. Regular monitoring (daily / weekly) of the work is planned according to the student’s progress and the tasks available.

Work packages (weekly schedule):

  1. Introduction to materials for fusion (W1)
  2. Training and introduction to density functional theory, molecular dynamics simulations and visualization tools (W2)
  3. Introductory problems with atomistic modelling code (W3)
  4. Simulation of fusion materials, post-processing, and results analyses (W4-W7)
  5. Report writing (W8)

Final Product Description:
The outcomes from the proposed project are key to improving our understanding of the fundamental properties of metals under irradiation and will show the possibility of simulating realistic large-scale metallic systems based on density functional theory (DFT) and molecular dynamics simulations (MD).

Adapting the Project: Increasing the Difficulty:
The project will evolve from relatively easy tasks which are already of high interest and that can be completed within a few weeks, towards doping in polycrystalline structures, which require larger atomic structures with more complex geometries.
Depending on the interest and previous experience, the student could also take active part in the development of interatomic potentials from density functional theory calculations. These simulations can start from simple polymorphs which can be reproduced with few atoms, and will progress towards complex amorphous and interfacial models of alloys and doped compositions.

Adapting the Project: Decreasing the Difficulty:
The range of materials and structures is quite broad, so the project can be readily adapted depending on the student’s interests and background experience. In case the analyses of dynamic models (time and temperature dependent) get too complicated or require too much time to converge, the study can be easily adjusted in scope to static models, from which we can extract valuable information like the equilibrium structure or the mechanical properties of the system. Working with static (frozen) models, we can make use of more complex and accurate interatomic potentials, and define real-scale structural models with a limited computing cost. Still, the study on the evolution of mechanical properties upon vacancy formation is an interesting topic and many structures can be analysed within the period allocated to this internship.

Resources:
The student will make use of BSC’s in-house resources like the MareNostrum supercomputer. We will preferentially use open source codes for modelling, simulation and analyses of the results.

Organisation:
BSC – Barcelona Supercomputing Center

Posted on by SoHPC Team Posted in Projects 2022 — No Comments ↓

Project reference: 2201

Loss of heterozygosity (LOH) is an evolutionary dynamic whereby heterozygous genomes progressively lose allele diversity according to natural selection. The result are genomic blocks of loss-of-heterozygosity (LOH blocks) where multiple homozygous alleles can be found in series. LOH blocks are often extracted from a genome to study its adaptation strategy to a specific environment. The block size, distribution, gene content and retained alleles are very informative in terms of how the species is adapting to the environment where it lives. In fact, the study of LOH blocks gained momentum during the last decade due to its importance in genome evolution, but this did not translate into a large amount of software developed for this purpose. The majority of studies carried out in this area are performed with self-developed scripts that never translate into a more general software that the rest of the community may use in the future. To fill this gap, in our group we are developing an algorithm named “JLOH” that is aimed at filling this gap, providing a general tool to extract LOH blocks from single-nucleotide polymorphism (SNP) data and a reference genome sequence. The core algorithm has been developed and already returned promising results on a few test sets, but extensive testing in different conditions must be carried out before opening this algorithm to the whole scientific community. The necessary testing will be done on the code’s: 1) scalability (CPU, memory), 2) ability to cope with different genetic properties (GC content, repeat content), 3) ability to cope with different data properties (coverage depth, SNP quality, SNP density). The testing will be conducted in the “MareNostrum4” HPC cluster at the BSC in Barcelona, providing the student with a state-of-the-art infrastructure to work with.

from Pryszcz et al. (2015) The Genomic Aftermath of Hybridization in the Opportunistic Pathogen Candida metapsilosis. PLoS Genet 11(10): e1005626. https://doi.org/10.1371/journal.pgen.1005626.
Heterozygous regions are in white, while homozygous blocks of at least 5 kb are depicted in grey. Loss of heterozygosity (LOH) detection is described in the paper’s methods. The method applied in Pryszcz et al (2015) is the ground algorithm of JLOH, the software that will be tested within the scope of this internship.
Figure copyright is not infringed as Toni Gabaldón is one of the authors of this paper

Project Mentor: Toni Gabaldón

Project Co-mentor:Matteo Schiavinato

Site Co-ordinator:Toni Gabaldón

Learning Outcomes:
At the end of the internship, the student will have gained substantial knowledge on the usage of an HPC cluster. The knowledge will be both in terms of day-to-day usage and in terms of good practices of data and workflow organization. The student will have familiarized with the standard procedures involved in developing and testing software and learned how to fully leverage the power of HPC in data analysis.

Student Prerequisites (compulsory):

  • Basic Linux shell skills
  • Basic knowledge of genomics

Student Prerequisites (desirable):

  • Understanding of python programming language
  • Familiarity with the concept of DNA variation (even if only from classes)

Training Materials:
The student is encouraged to use the many free online resources available at websites such as “tutorialspoint” or “codeschool” to get familiar with:

  • The GitHub environment
  • The basics of an HPC cluster, e.g. the SLURM queuing system

Prior knowledge is not needed, and these will be addressed together during the first week. It will however be very useful for the student to familiarize with the concepts before the internship.

Workplan:

  • Week 1 (training week): the student will learn the basic functioning of the algorithm and familiarize with the MareNostrum4 HPC cluster, closely helped by the research group.
  • Weeks 2-3-4: testing the scalability of the software in terms of computational resources using pre-existing data, submitting a workplan by week 3.
  • Weeks 5-6-7: the student will scan the literature for available datasets that can be used to test the tool, simulate further data to add to this collection (if time permits), and test the software with these datasets.
  • Week 8: Summary of the experience, wrap-up, submitting a final report by week 8.

If two online students are selected, since online supervision may be less effective, one student will take care of the scalability testing and the other of the dataset testing for the duration of the internship.

Final Product Description:
This study is a necessary step in software development. Its results will attest to the core algorithm’s ability to carry on its function in multiple conditions, on different data, and fully using the available computational resources. If the results will be incorporated in a scientific publication, the student will be considered a co-author of it.

Adapting the Project: Increasing the Difficulty:
In case difficulty must be raised, the student(s) will be asked to simulate testing data under a larger number of variables, finding potential bugs in the software and increasing the scientific value of the project results.

Adapting the Project: Decreasing the Difficulty:
In case students will need more training than expected, an extra week will be dedicated to teaching them more of the HPC basics and good practices. The work will be limited to scalability testing and non-simulated data securing an outcome for the student(s) and for the group.

Resources:
The student will need a computer with a Linux-based operating system or, at a minimum, access to a terminal. If in presence, this can be provided by the institute or the research group. The student will be granted access to the MareNostrum4 at the BSC. The data and computing hours used by the student will be placed under the projects of prof. Gabaldón.

Organisation:
BSC – Computer Science- European Exascale Accelerator

Posted on by SoHPC Team Posted in Blogs 2022 — No Comments ↓

Applications will be open in February 2022. See the Timeline for more details.

PRACE Summer of HPC programme is announcing projects for 2022 for preview and comments by students. Please send questions to coordinators directly by the  mid February. Clarifications will be posted near the projects in question or in FAQ.

About the Summer of HPC programme:

Summer of HPC is a PRACE programme that offers summer placements at HPC centres across Europe. Up to 40 top applicants from across Europe will be selected to participate in pairs on 24 projects supported and mentored online from 11 PRACE hosting sites. Participants will spend two months working on projects related to PRACE technical or industrial work to produce a visualisation or video. Programme will run virtually from 29th June to 31th August 2022.

For more information, check out our About page and the FAQ!

Ready to apply? (Note, not available until mid February, 2022)

Have some questions not found in the About section or the FAQ? Email us at sohpc16-coord@fz-juelich.de.

Programme coordinator: Dr. Leon Kos, University of Ljubljana

Posted on by Regina Mumbi Gachomba Posted in Blogs 2021 — No Comments ↓

Hello everyone!

As you can tell from the title, this will be my final blog post submission. I will be giving more details about the MCPU, as promised on my previous blog post which you can read here if you haven’t.

So let’s get started!

The Memory Tile

Illustrated above is the basic structure of the memory tile I worked on simulating using Coyote. The memory tile houses the MCPU (Memory Central Processing Unit), which can loosely be described as the ‘intelligence’ of the memory tile, responsible for organizing resources that are needed to perform the different memory operations.These resources are obtained from the microengine, the vector address generator (VAG) and within the MCPU itself. The microengine is responsible for generating transactions for the instructions, whereas the vector address generator generates the memory requests. Another impressive feature of this memory tile is that it allows the re-usability of some already implemented functionalities. For example, a scalar load operation is handled like a unit stride vector load with a loop iteration of 1.

My primary objective was to understand how instructions, commands and data packets are to be received into the memory tile. Once an overall understanding of the architecture was established, our goal was to simulate the different load and store operations (shown below) and analyse their output and performance.

Below is the video presentation my partner Aneta and I submitted for our project presentation. In it , we have discussed how the memory operations and scheduling processes are implemented in Coyote:

Before I leave …

The past two months have been the most exciting for me this year. I have had the opportunity to learn a lot from the internship and my able mentors. I have also established an interest in high-performance computing and I look forward to exploring this interest further in the near future. To you who is reading, I hope you enjoyed reading my blogs as much as I enjoyed writing them, and I also hope you learnt something new. I would like to thank my mentors at BSC, my partner Aneta, PRACE and you ,the readers for the guidance and support 🙂

Adios!

Posted on by Sepideh Shamsizadeh Posted in PRACE Summmer of HPC 2021 — No Comments ↓

After two months of daily meetings and work with my collueges, we are at the end of the project. These months, I learned a lot about supercomputers and machine learning. It was a really great experience for me to get familiar with challenges and use my theoretical knowledge in a real-world experience. I have had the opportunity to work on Cineca and I am so grateful for that.

I had some experiences with big data and deep learning projects, it was my first time using this knowledge for detecting anomalies. Our daily meetings were so informative and useful. Machine learning and deep learning were my more interesting courses during my master’s. I always loved to use them for a real-world project and this summer was my opportunity to use them.

In summary, my task was optimizing a new deep learning model for detecting anomalies. Here is the final presentation video so you can take a look at it:

I will save my contact with my new friends from summer school even I could find this chance to visit CINECA in person.

Posted on by Paolo Scuderi Posted in Blogs 2021, FAQ, PRACE Summmer of HPC 2021, Projects 2021 — No Comments ↓

Here we are again for the third time! Last time! What an amazing summer was! Now it is September, new projects will start as soon as possible and new adventures are waiting for me. But before going on I would like to talk in my last blog post about something useful I learned and why you should apply for this program.

Computational Fluid Dynamics Tools

In general, a fluid dynamics computation is made up of three different steps: pre-processing, simulations, post-processing.

  • Pre-processing: in this part, we performed our mesh, composed of up to 46 million fo tetrahedral elements. To create the mesh, we used ANSA. Unfortunately, this is not an open-source tool, but it is available in the student version. My mate, Benet Eiximeno Franch, who has been a student during this program, provides to the team the meshes for the three different geometries.
  • Simulations: this is the crucial part of the work. We selected to use OpenFOAM, which is an open-source CFD solver widely used for research activities and industry projects. We used the simpleFoam and pimpleFoam algorithm in order to evaluate the solution for the steady-state and the transient simulations, respectively. We selected to use, according to our Supervisor Ezhilmathi Krishnasamy, the RANS model based on the two equations k-Omega SST turbulence models. We also tested other turbulence models and, in the final paper, we had compared the results. What we noticed is the according to in the wake region of the k-Epsilon and the k-Omega SST. Instead, the k-Omega differed a lot from the other as a consequence that it is used to predict well the flow near the wall, while the wake region is a free zone far from the wall, indeed the k-Epsilon compute well the solution.

Q-criterion

This is one of the typical visualization used to figure and draw the vortices. To understand the main idea I will explain how we computed it. Starting from the definition of the gradient of the velocity field, we can split it into two tensors: one symmetric and one antisymmetric. The first one is associated with the strain rate, while the second one is linked with the rotational capabilities of the fluid element that we are considering

Splitting the velocity gradient.

From these definitions, we can build the scalar Q value as shown

Scalar Q-value

where “tr” stands for the sum of all the diagonal elements of the matrix. In this way, it is easy to understand what it shows when it is positive or negative. In particular, we have

  • Q<0: areas of higher strain rate than vorticity in the flow
  • Q>0: areas of higher vorticity than strain rate in the flow

The figure below shows what is explained for Q=10 for all the three configurations: Fast-, Estate-, and Notch- -Back.

Steady-states Q-criterion for the three back geometries.

Overview of turbulence modeling

I already discussed it in my previous blog post. You can check it here.

Blunt body incompressible aerodynamics

Cars are blunt bodies. For that reason, when the Reynolds number is very high and we are considering an incompressible turbulent regime, a particular phenomenon appears. This is called the crisis of resistance, in which suddenly the CD decreases. This is also the reason why the golf balls have small pits in order to accelerate the transition of the flow from laminar to turbulent making appeared the previously mentioned effect and reducing the drag. In addition, for that reason, the CD remains almost constant with the variation of the Reynolds number. We performed several simulations for all the configurations for three different Reynolds numbers. In the picture, you can see these effects. However, if you are interested, you can ask us for the final report paper and we will send you all the details.

CD-Reynolds graph. Comparison of F, E, and N.

Rear Mirror streamlines

We analyze also the rear mirror effects on the three different geometries. You can follow the video to understand better. Anyway, I would like to give you a short introduction with the following image.

Rear mirror streamlines.

Final results

Our final results are published in our final report that you can find on the main page of the PRACE Summer of HPC programme. Here, I would like to share with you our recorded final presentation that we made on the 31st of August 2021.

Final presentation.

Why should you join SoHPC?

Generally speaking, SoHPC is an enjoyable program. In this experience, you will learn in the first week the main concepts of High-Performance Computing with lectures hosted by one of the most important HPC research institutes around Europe. In our case, we have the pleasure to be welcomed by the ICHEC, in Ireland. We learned many important things in such a short time, as different techniques to program, python, key access.

Then, you will be divided into different teams, one for each project. You will have the pleasure of working and meeting other guys from all over Europe with passions similar to yours: HPC, coding, and, in my case, fluid dynamics. But the HPC projects that SoHPC offers are regarded in many scientific areas of interest: fluid dynamics, big data, machine learning, FEA, Earth observation, parallelization of codes, etc.

In the project you will work on, you will have the possibility to have the access to one of the HPC clusters in Europe. You can work on what you love and learn much surprising stuff. Apply and let me know!

You can contact me on LinkedIn: Paolo Scuderi. I am looking forward to talking with you!

Click Paolo Scuderi

Posted on by David Mulero Perez Posted in Blogs 2021, PRACE Summmer of HPC 2021 — No Comments ↓

After two months of hard work, the time has come to say goodbye to this project. I have had the opportunity to work on the visualisation of one of the most powerful supercomputers in Europe and I could not be more grateful for that.

Since I started my Multimedia Engineering degree I have been fascinated by the different ways to generate graphics and how useful it can be, from creating a web page, a mobile application, to a C program. This time I have used Python and the VTK package to generate these graphics and I am very happy with the result as it was a technology I had not tried before and I have achieved the objectives. Here is the final presentation video so you can take a look at it:

Finally, since it has not been possible to do so for the last two months, I am going to visit CINECA and I will be able to see in person the supercomputer I have been working with. I think there can be no better ending than this farewell trip.

(Tramadol)

(messinascatering)

Facebook
Twitter
Follow by Email