Nanotube-laboratory in a computer

I spent the first few weeks at Computing Centre of the Slovak Academy of Sciences getting familiar with the nanotube code. We actually changed the goal of the project a bit. The original plan was the further development of the MPI parallelization, but now I am working on an extension of the code with a new feature. The task is to compute (and visualize) the electron density of the orbitals that come out of the simulation.
In this blog post, I am giving a short introduction to quantum chemistry in general, and I will tell about the interesting things I have learnt about nanotubes.
How to make a nanotube in 3 easy steps
Due to their extraordinary properties, nanotubes are in the focus of material science, nanotechnology and electronics as well. Carbon nanotubes are cool things indeed: they are one of the strongest materials, they can behave either like metals or semiconductors, they have good thermal conductivity, and they are the material of Vantablack, too.
You can make a nanotube this way in a thought experiment (the real synthesis is not this, of course):
- Step 1: Take a layer of a two-dimensional periodic material, for example, a sheet of graphene. Periodicity means that you can construct the whole material by translating a repetitive unit, the unit cell. In the picture, the unit cell (blue) contains two carbon atoms, and has two unit vectors.
- Step 2: Define the rolling vector (purple) by connecting the centers of two unit cells of the graphene sheet. Cut out a rectangle whose one side is the rolling vector.
- Step 3: Roll up the nanotube by connecting the two ends of the rolling vector.
Congratulations, now you have a carbon nanotube!
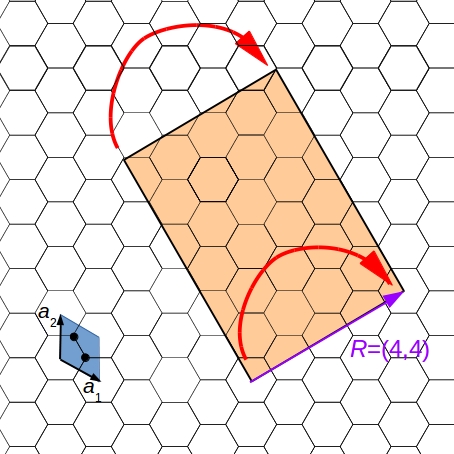
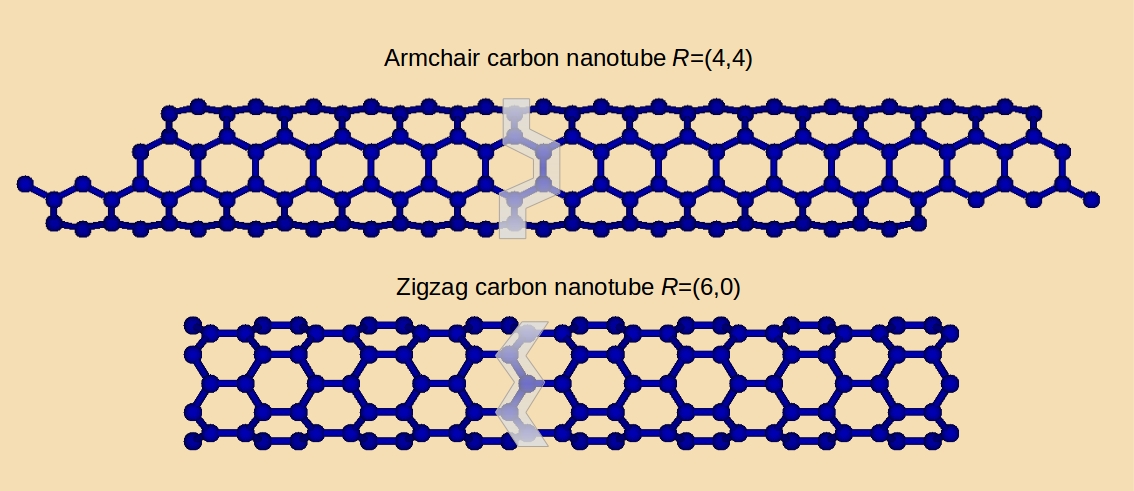
Its material and the rolling vector characterize the nanotube. The rolling vector determines the diameter, the structure (armchair, zigzag or chiral), and the conductivity (metallic or semiconducting).
Quantum chemisty in a nutshell
The potential engineering applications made the nanotubes an important topic of computational science. I am working on a code that computes the electronic structure of the nanotube. But before going into details about the particular code, I would like to tell you about quantum chemistry in general.
Some people, who asked me about my field within chemistry, were really surprized when I told them I am not working in a laboratory, but I am doing computer simulations. They were thinking that chemistry is only about boiling colorful liquids in flasks and experimenting with explosives. But it is not true, at least for the last few decades, the age of computational quantum chemistry. Applying quantum mechanics for molecular systems helps us to explain many experimental phenomena: Why can the matter absorb light only at certain wavelengths? Why can two atoms make a bond? What is the mechanism of a chemical reaction on the molecular level?
The first step to answer these questions is to solve an eigenvalue-equation. In quantum mechanics, we always solve eigenvalue-equations, because physical quantities are described by operators whose eigenvalues are the possible values of the physical quantity, and the quantum states are described by the eigenvectors. The Hamiltonian operator is the operator of the energy, and its eigenvalue-equation is the famous Schrödinger-equation.
Unfortunately, the Schrödinger-equation can be solved analytically only for simple (model) systems, for more complicated cases we do it numerically using computers. How is it done in practice? The wave function will be the linear combination of some basis functions and the Hamiltonian is represented by a matrix. Then, we diagonalize the matrix to get the basis expansion coefficients and the energy.
Goal: Electron density of the nanotube
So, we have the nanotube code that computes the energy of the electron orbitals. My task is to construct the orbitals and the electron density from the basis function coefficients. Electron density tells us the probability of finding the electron at a given point. This way we can visualize the chemical bonds and the nodes of the orbitals. Now, I am working on the serial code and testing it on simple systems like benzene, and I get plots like the one below.

This is enough for now maybe, I will write about the nanotube code and how we do the electron density computation (and hopefully some results) in the next blog post.
