Solitaire Games, Neutron Diffusion and Quantum Mechanics


We are approaching to the fancy parts of my project named “Hybrid Monte Carlo/Deep Learning Methods for Matrix Computation on Advanced Architectures”.

After World War 2, the story started with “a simple question” from a great scientist named Stanislaw Ulam.
In his convalescence days, he entertained himself by playing solitaire games.
While playing, the question “ What are the chances that a solitaire laid out with 52 cards will come out successfully?” appeared in his mind.
This question started an interest in determining the probability of winning and calculating the outcome of each event in the game. With this interest, he explained the rest with his words:


When he shared his ideas with John von Neumann who is also a great scientist, they decided to name the method after the gambling spot in Monaco, “Monte Carlo”. The first formulation of Monte Carlo computation for an electronic computing machine was outlined by Neumann to solve neutron diffusion and multiplication problems.

Since then, Monte Carlo Method helps to simulate the experiments with the outcome. The magic behind the Monte Carlo Method is repeating the experiment with random sampling. As long as you repeat the experiments, the results will be better.
Nowadays, Monte Carlo is an important and handful method for finance, physics, and even Quantum Mechanics.
Consequently, Monte Carlo Method became one of the most important factors for the birth of High-Performance Computing.

Let’s start with the classic example: Estimating Pi with Monte Carlo
Imagine you are playing dart with this funny board:
[Adapted from the reference: nicoguaro, CC BY 3.0, via Wikimedia Commons]
Imagine the darts are only allowed to hit inside of the square with 1cm² area, and the darts that hit inside the quarter circle with π/4 cm² are counted. If of the number of darts that hit inside the quarter circle divided by the total count of darts (n) thrown, and multiplied by 4, pi can be estimated.
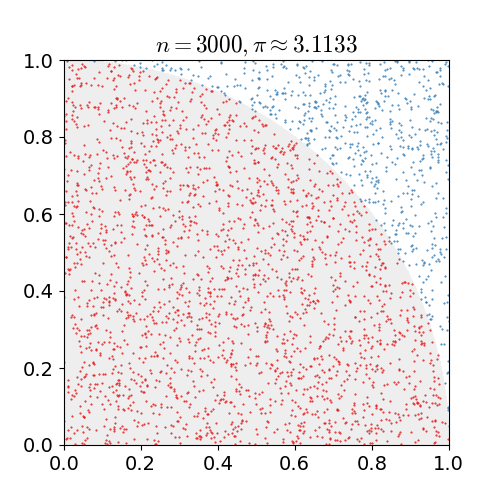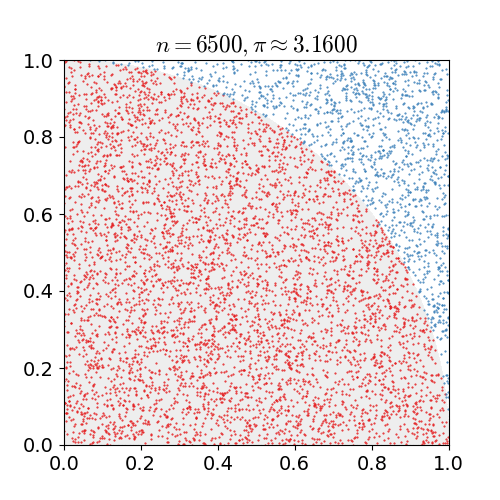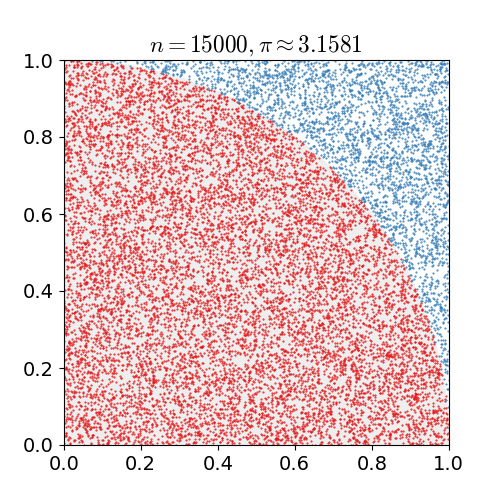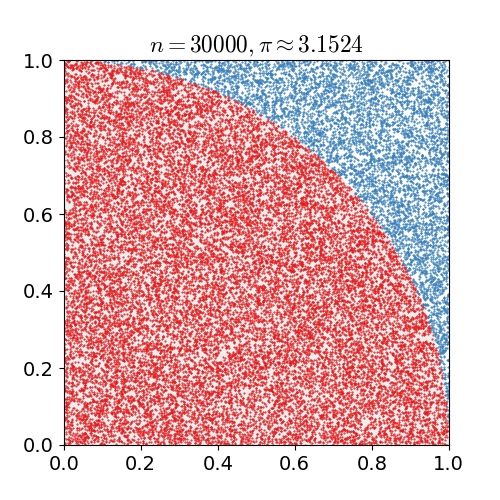
[Reference: nicoguaro, CC BY 3.0, via Wikimedia Commons]
However, you need to throw too many darts to have a good estimation,
and nobody likes to wait for the calculations.
That’s why High-Performance Computing is also important.
Did you like the Monte Carlo Method and HPC?
If you are interested with High-Performance Computing, why don’t you look at the PRACE Tutorials.
to be continued…

You can really explain as simple as possible, all of the complex things like this. That’s why i like your posts. keep writing and good luck on your project 🙂