What do we want to know about a solid?

You may wonder how can we study and, more importantly, predict a material feature such as mechanical stability, thermal conductivity and so on. The answer is: solve the Schrodinger equation! Simple right? Right? … Well not that easy. The most complex system that we know how to solve exactly is the ionized hydrogen molecule. A solid system has billions and billions of atoms and electrons that is impossible to solve by hand. That’s why we use supercomputers. But there are many ways to solve the Schrodinger equation. One of the most used is Density Functional Theory ( DFT ). This method is based on the electron charge density and, without going into details, within some reasonable approximations, it allows as to know precisely all the dynamical, thermal, … In short all the properties of a material.

In my project “Heat transport in novel nuclear fuels” the supercomputer of Ostrava IT4Innovation National
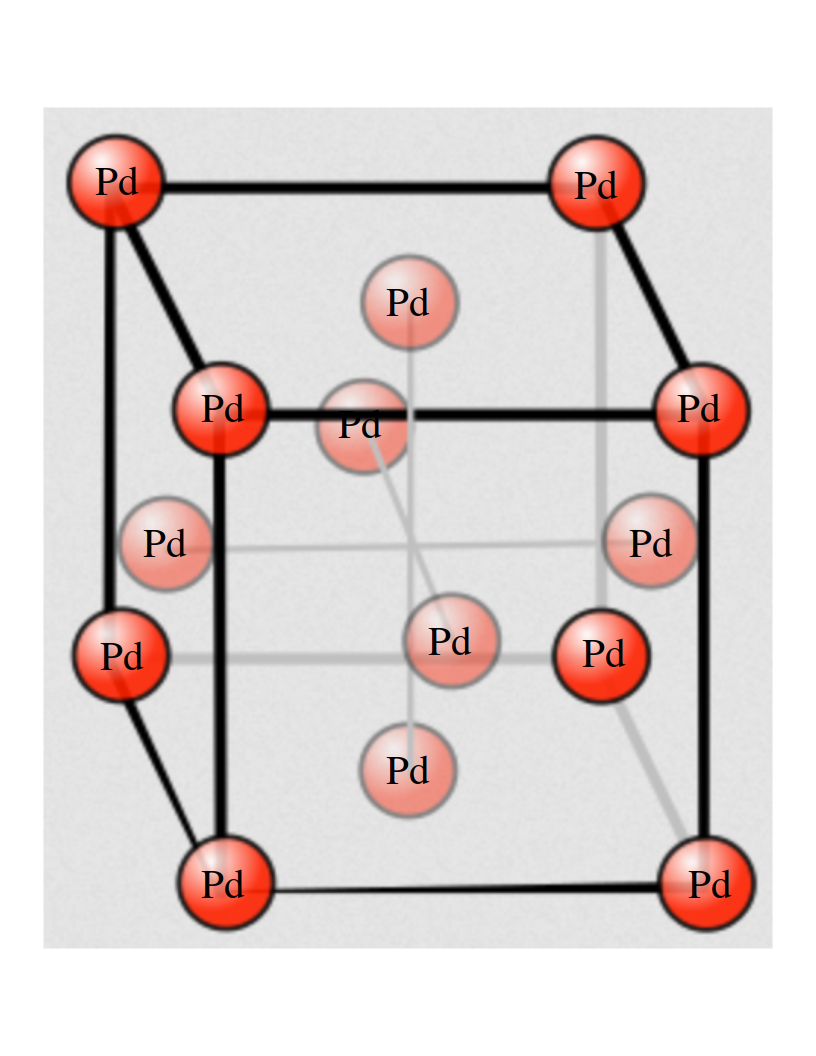
Supercomputing Center comes to our aid. I used the Vienna Ab-Initio Simulation Package (VASP) software module, that simply implements DFT, to look into the well known properties of palladium, as an exercise, that I now want to share with you. First of all let’s look at the structure of Pd. It is known as Face Centered Cubic (FCC) and it looks like this:

Other important features are the mechanical ones. How much can I stretch a solid? After what pressure it brakes? This features can be calculated “by hand” changing the input files. An important parameter of the structure of a solid is the lattice parameter (a) that is the side of the cube you see above. Changing it means to dilate the material and to see how the energy per atom (E) depends on it is related to the answer to the questions above. This E(a) curve determines the mechanical properties of the material.

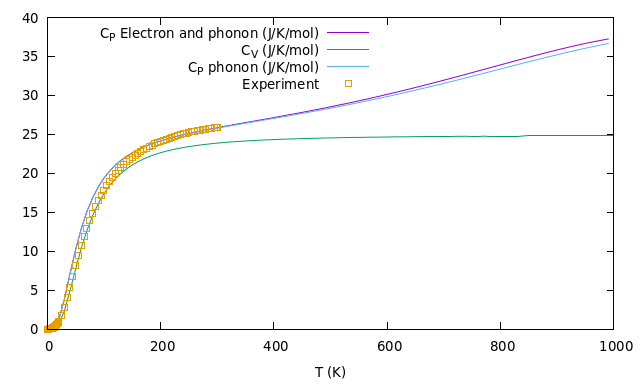
What about the thermal properties? There is a general one to one correspondence between temperature and vibrations of particles. The more particles moves the higher is the temperature. So, in a solid, it’s important to look at the motion of electrons and phonons (just a name for quantized vibrating nuclei motion). What it’s calculated is the so called dispersion diagram, i.e. the relation between the energy (or frequency) of a particle and its momenta. This is important to understand how many states are present at a certain energy (the Density Of States) and consequently all the thermal properties. An example of a theramel feature of a solid is the Heat Capacity at constant pressure, C_p, that, most importantly, is measured in experiments. Below I report what I computed on the supercomputer versus some experimental results as an example of the great reliability of DFT.

In the next weeks me and Luigi will investigate the properties of possibly the new generation nuclear fuels thorium and uranium sesquicarbide Th₂C₃ and U₂C₃. What is important in this study is to understand how the presence of carbon atoms in thorium and uranium compounds effect the heat transport feature. This will tell us if carbons increases or decrease the thermal conductivity (i.e. the efficiency) in a possible nuclear fuel. Anyway, thanks for your attention and see you next weeks! Hopefully we will update our blog soon with great results!