A short tour of lattice QCD

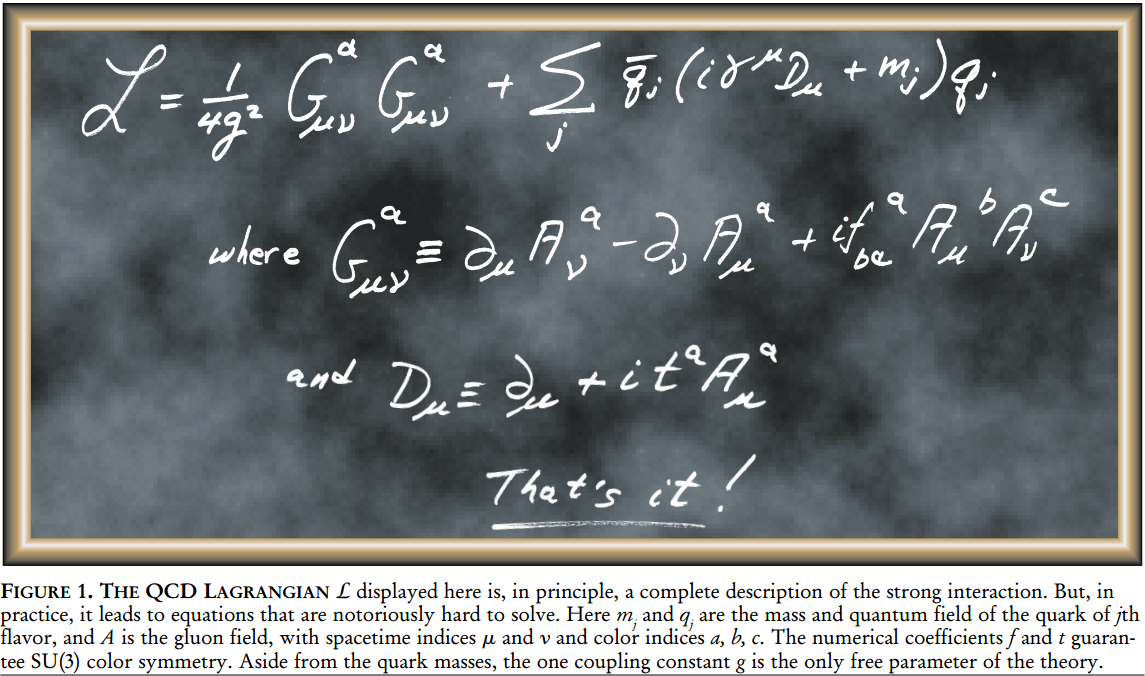
As my first blog was completely non technical I am now contractually obliged by the powers that be to talk about some technical stuff of what I am actually doing. I decided I would have a go at explaining what lattice QCD actually is and how we use it. But before I can do that though I need to first explain what plain old Quantum Chromodynamics (QCD) is and why we need to put it on a lattice. A disclaimer is in order though, as with all popular science writing done in this fashion, it is impossible to be precise and there are is a good chance some things I write might be not 100% true.

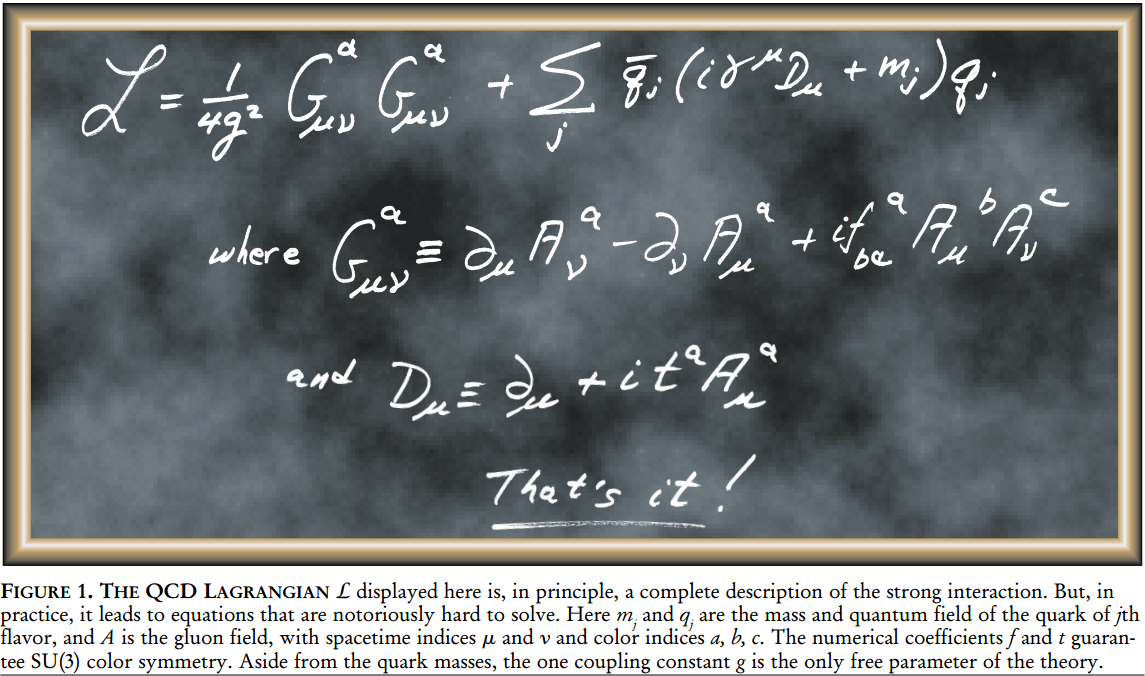
Source:  http://frankwilczek.com/Wilczek_Easy_Pieces/298_QCD_Made_Simple.pdf

Pictured above is the QCD lagrangian that appears in the standard model of particle physics, describing the theory of the strong interaction, it is one of three interactions described by the standard model, the other two being the weak interaction and the electromagnetic interaction. Similarly to a more familiar part of the standard model, Quantum Electrodyanmics (QED) describing the electromagnetic interaction and it’s corresponding electric charge, particles which posses “colour charge” participate in the strong interaction. Unlike electromagnetism however is that there are 3 different colour charges named red, green and blue, it should be noted that they have nothing to do with actual colour and are just a handy naming convention.

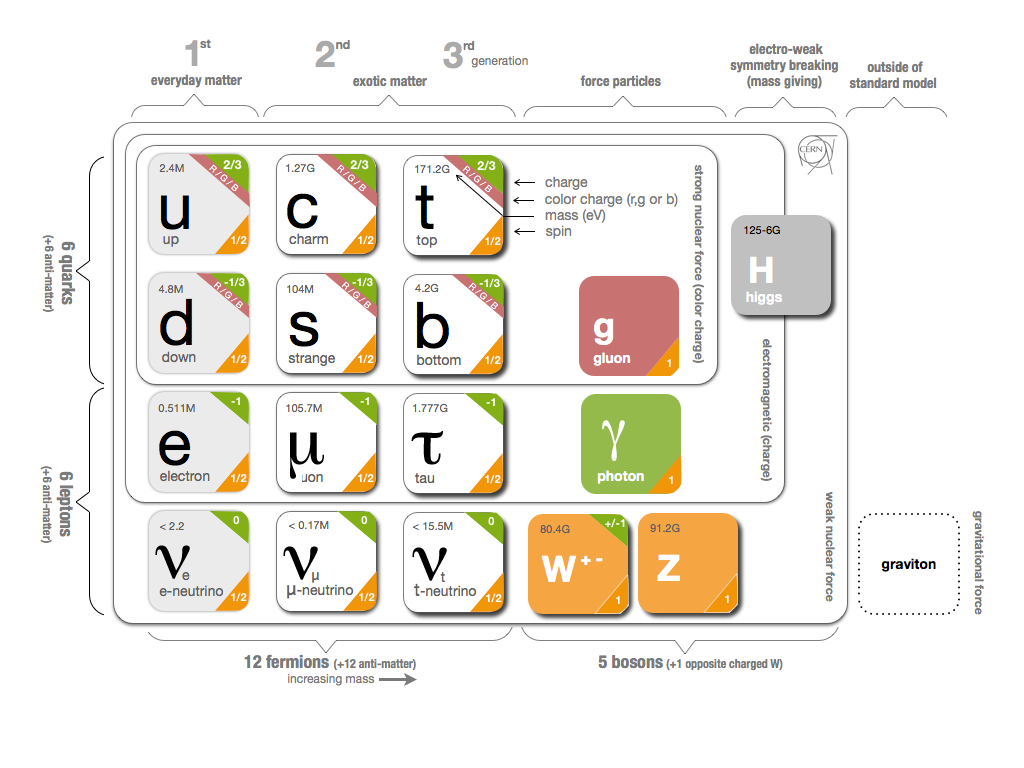
Source: https://cds.cern.ch/record/1473657/files/SMinfographic_image.png?subformat=

Of all the particles in the standard model pictured above the only ones which carry the colour charge are the quarks and the interaction carrying gluons, with there being 6 known flavours of quarks; up, down, strange, charm, bottom and top with each having a possible 1 of 3 colours as well as their antiparticles and also 8 different “mixed colour” gluons. Another striking difference between QCD and QED is the fact the gluons themselves carry the colour charge where as the photons which transmit the electromagnetic interaction do not. This “self interaction” leads to a lot of the unique characteristics of QCD. Another difference is simply how strong the interaction is compared to electromagnetism and the weak interaction, the strength of these interaction is determined by a coupling constant (the g in the first image of the lagrangian), for electromagnetism the number is approximately 0.007, known as the fine structure constant, for the strong interaction however the coupling strength is approximately equal to one for normal energies in the standard model (<2GeV) and is precisely the reason it is called the strong interaction and why we need lattice QCD.

These different properties of the theory lead to some very unique phenomenon, Confinement and Asymptotic Freedom being two. Confinement is the fact that the the force between quarks does not diminish as they are separated, in fact it grows linearly. Because of this, when you try to separate two quarks the energy in the gluon field is enough to create another quark anti-quark pair; thus quarks are forever bound in the strongly-coupled region into composite particles (hadrons) such as the proton, the neutron or the pion. Although analytically unproven, confinement is widely believed to be true because it explains the consistent failure of free quark searches, and it is also demonstrable on the lattice. Asymptotic Freedom means that at very high-energy quarks and gluons interact very weakly together (the coupling goes to zero) and are almost like free particles, this explains the commonly seen phenomenon of the narrowness of high energy jets in particle collider reactions.

As I mentioned previously coupling constant of approx 1 at normal energies, this presents a big problem for standard methods of calculation in Quantum Field Theory (QFT). Without going too in depth, calculations are typically done using ‘perturbation theory’ which basically means expressing our answer as an infinite series in powers of the coupling constant.  For QED we have a coupling constant of 0.007 so each consecutive term is significantly less important. But for QCD at everyday energies we have a coupling constant of about one so each term is just as important (in reality we can only create the series if the coupling constant is less than 1). So we turn away from perturbation theory to lattice QCD to solve our problems. Lattice QCD also helps remedy another major issue that arises in QFT, infinities, QFT’s are rife with infinities that require a range of techniques to deal. Naively these infinities arise from two separate but related infinities in the real world, the infiniteness of space (known as infrared divergences) and the fact it is continuous(known as ultraviolet divergences). Happily putting our theory on the lattice does away with both these infinities in one go. We put our whole space into a box of finite volume and we discretize the space into a finite number of points. Of course lattice QCD isn’t some magical tool and we don’t solve all our problems for free, newer problems do arise but these are manageable enough to preform calculations.

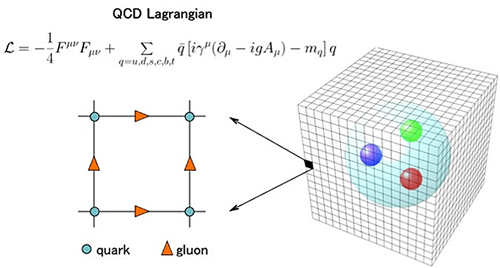
Source: http://lpc-clermont.in2p3.fr/IMG/theorie/LQCD2.jpg

So using this idea as well as wick rotation we end up with something that we can actually simulate on a computer which should, in the limit that the lattice spacing goes to zero and the volume goes to infinity, give correct physical results.