Building a reliable model from just a few observations

Welcome to my final blog post on the PRACE SoHPC website! First, I will show you a trick I used for building an accurate model from few data observations. Then I will  introduce the video presentation that summarises my work during this summer at the Juelich Supercomputing Center, that was shown during our final web conference.

Introduction

In my last post we saw that we needed a way to create some kind of model from a set of data points. Specifically, we needed to tune the Acceptance rate (the dependent variable) by manipulating the number of MD steps (the independent variable), whose relationship is unknown. Not only is it unknown, but there are some other parameters, such as the lattice size, that we know can influence this relationship for different simulations. Therefore, we concluded that an online algorithm would make things simpler, as the model would have to be created from observations by using the same combination from the remaining parameters.

However, we are not completely unaware of the relationship we are looking for. From my last post we saw that:

• the data have a sigmoid or an S-shaped (almost)
• the acceptance rate (dependant variable) starts from 0.0 for a few steps and ends at 1.0 for a big number of steps.

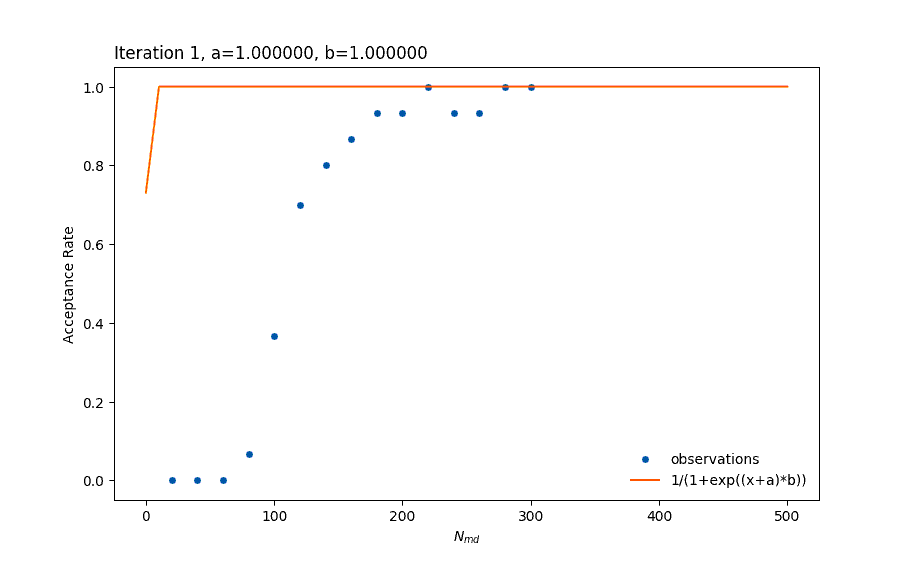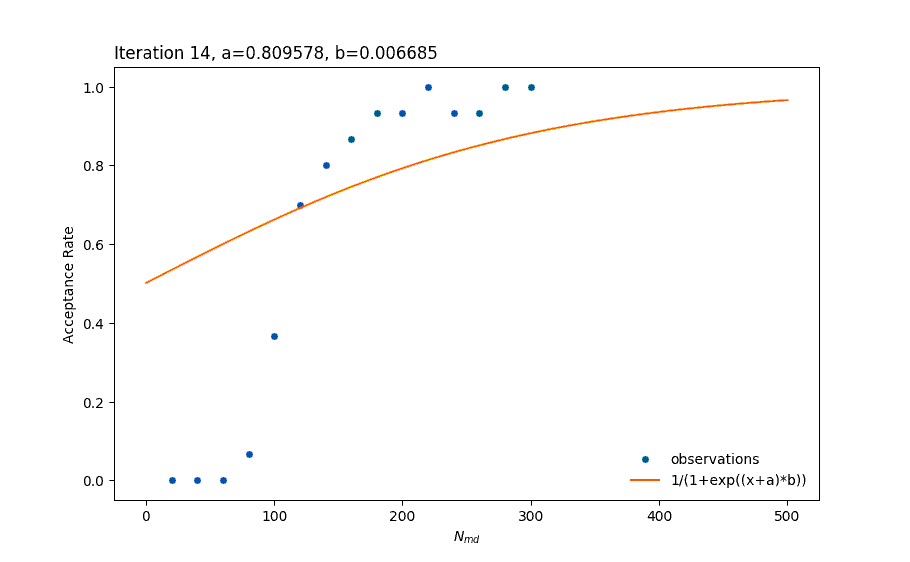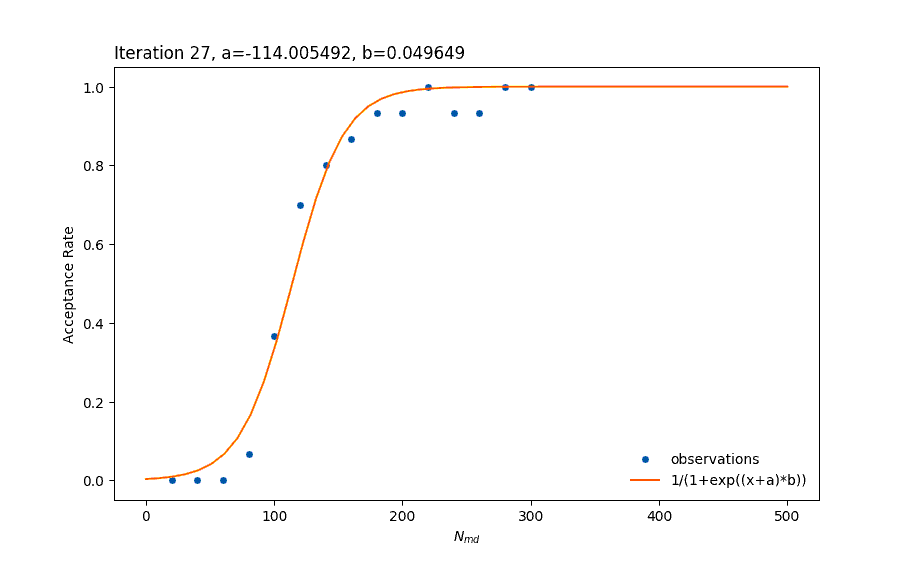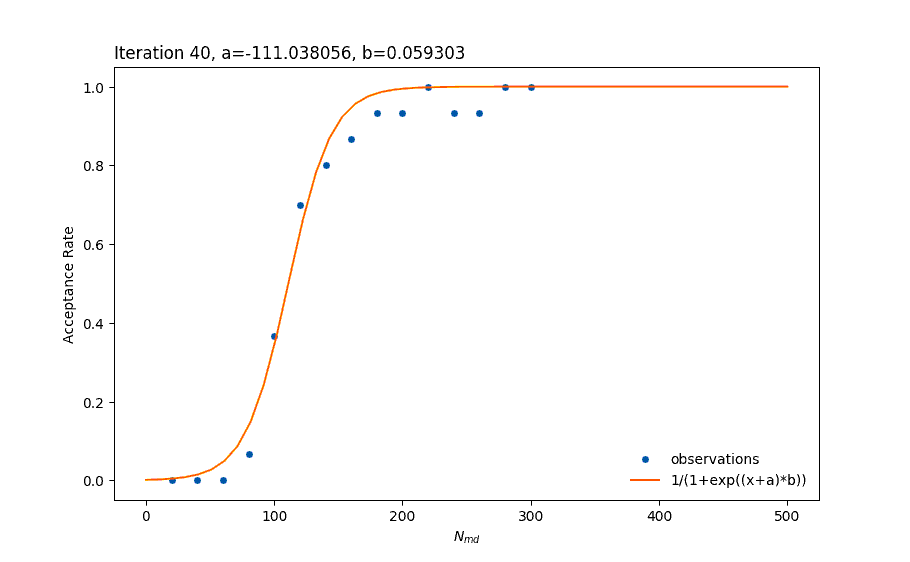
There are many ways of creating a model, such as regression by using a Multi-Layer Perceptron (MLP) – which is a type of an Artificial Neural Network. The problem with such an approach is that neural networks are very agnostic to the shape of the data we would like to model. It can take longer to train the network and it is also prone to overfitting (the error of the training data contributes to creating an inaccurate model). The biggest disadvantage of using the neural network approach is that since it doesn’t take into consideration what we already know about the shape, it can give a model that fits the current data well but makes very bad new predictions (such as with overfitting). Imagine the orange line in the above figure to be the result of training an MLP, but for any Nmd greater than 300 the acceptance rate falls back to values near 0. This is very possible with MLPs and it is unwanted. That is one important reason for choosing to fit the data to a specific function by using least squares fitting instead.

Selecting the best function for fitting

In the above picture, we saw an attempt to fit the data to the equation 1/(1+exp(x)) which was a relatively good attempt. The problem though is that the sigmoid function is symmetric. As we can observe, the orange line is more “pointy” than needed at the top part of the figure and less “pointy” than needed at the lower part. The idea was to look for functions that look like a sigmoid function but allow for a degree of asymmetry. The solution was to use the Cumulative Distribution Function (CDF) of the skew normal distribution.

The CDF gives the area under the probability density function (PDF) and it actually has the shape we are looking for. Also, the skew normal distribution allows skewness which can make our data better fit the model. In the following graph, you can see a comparison of the normal distribution and the skew normal distribution.

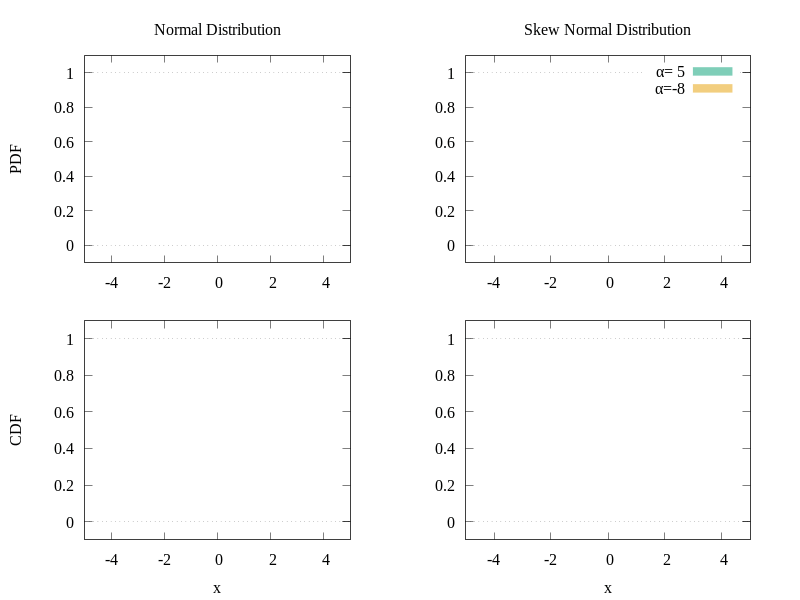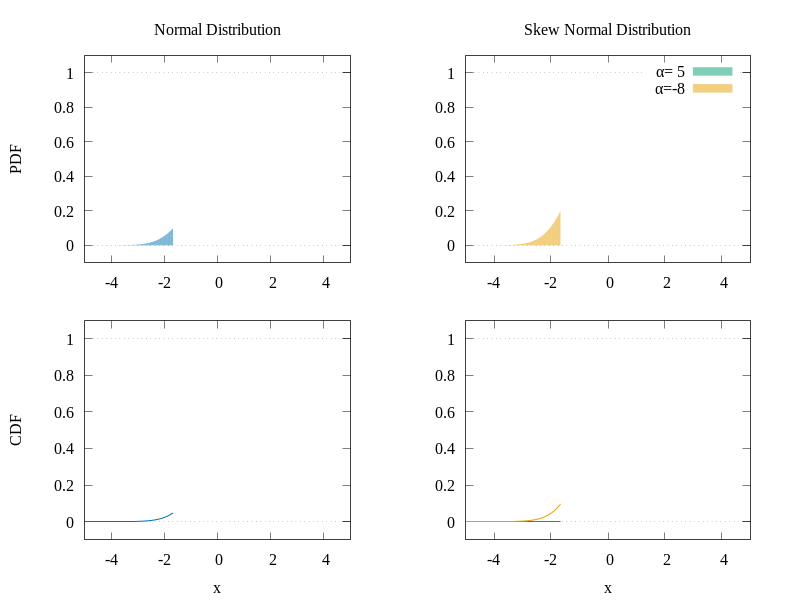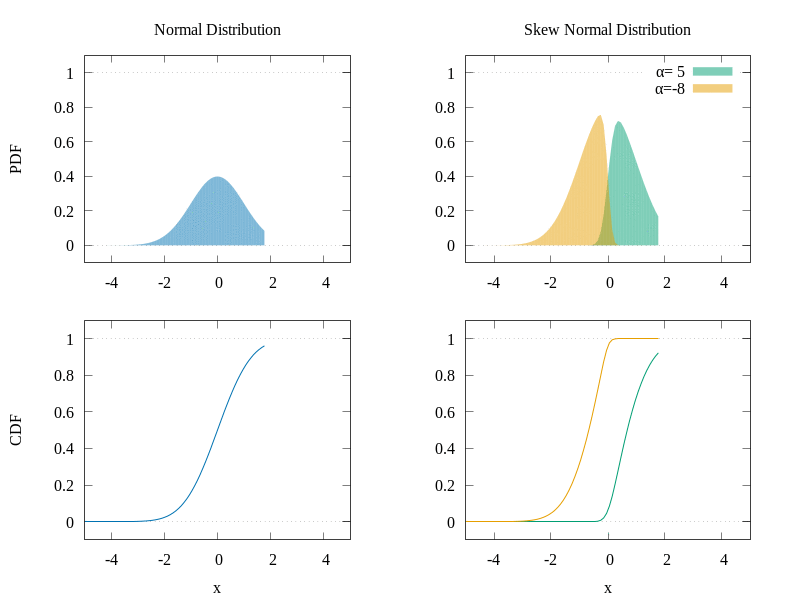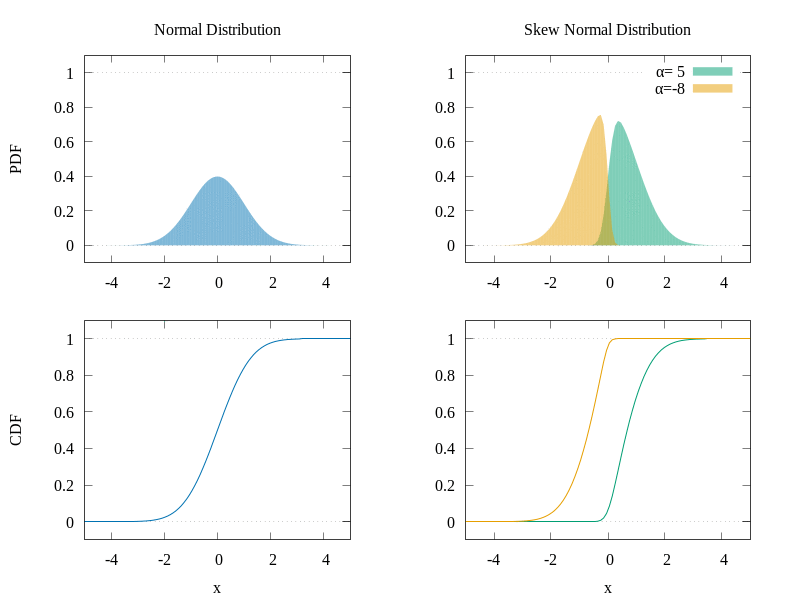
Comparison of the PDFs and CDFs of two distributions.

As we can see, by manipulating the α parameter, we can change the shape of the PDF of the distribution and consequently the shape of the CDF as well. Of course, as the selection of the function was done visually, it does not necessarily mean that the physics give a skew normal distribution form to the data, but it seems to suit our cases well. In the following figure, we can see a demonstration of the different CDFs we can obtain by varying the α parameter.

This “trick” gave a quick and accurate methodology for creating a relatively good model, even with a couple of observations.

Video Presentation

And now I present to you my video presentation that summarises the work. At the 3:56 timestamp, you can see the resulting visualisation of the tuning in action.