Learning to track objects in 4D data

At the time when I wrote my last blog post (check it out if you didn’t read it!) I was quite happy with the state of my Summer of HPC project “Tracing in 4D data“. I had completed the implementation of a 3D version of the object tracking algorithm Medianflow and the test results of the dummy data were quite promising.

That changed when I got the results when using real world data. The problem was not so much the tracking accuracy of the algorithm, which actually was quite good, but it was the performance. The execution time was very problematic: 25 minutes to track one bubble between two frames? We need to track hundreds of bubbles through hundreds of frames! OK, we can track every bubble independently so a parallel implementation of the algorithm would scale quite well with the number of bubbles, but that’s not true for the number of frames!

I felt that a more advanced tracking algorithm could perform much better, while still retaining the same advantages from parallelization. That is why I considered OpenCV again, to select another algorithm to generalize to three dimensions. I found KCF, which stands for Kernelized Correlation Filters.

Again, if you’re not interested in the math, you can skip directly to the last section where you can see some nice visualizations of the testing results of the algorithm! Or if you don’t want to read at all, just watch the video presentation of my project here:

Kernelized Correlation Filters

The second algorithm I chose to implement is KCF [1]. While MedianFlow is based on old techniques of Computer Vision (it’s based on the Lucas-Kanade feature tracker [2] which was originally published in 1981), KCF is inspired by the new statistical machine learning methods. It works by building a discriminative linear classifier (which some people would call artificial intelligence) tasked with distinguishing between the target and the surrounding environment. This method is called ‘Tracking by detection’: the classifier is typically trained with translated and scaled sample patches in order to learn a representation of the target and then it predicts the presence or absence of the target in an image patch. This can be very computationally expensive:

• In the training phase, the classifier is trained online with samples collected during tracking. Unfortunately, the potentially large number of samples becomes a computational burden, which directly conflicts with real-time requirements of tracking. On the other hand, limiting the samples may sacrifice performance and accuracy.
• In the detection phase, what happens then – as with other similar algorithms, is that the classifier is tested on many candidate patches to find the most likely location. This is also very computationally expensive and we encounter the same problems as before.

KCF solves this by using some nice mathematical properties in both training and detection. The first mathematical tool that KCF employs is the Fourier transform by taking advantage of the convolution theorem: the convolution of two patches is equivalent to an element-wise product in the Fourier domain. So formulating the objective in the Fourier domain can allow us to specify the desired output of a linear classifier for several translated image patches at once. This is not the only benefit of the Fourier transform because interestingly, as we add more samples the problem acquires a circulant structure. To better explain this point, let’s consider for a moment one dimensional images (basically vectors). Let be a 1-D image. The circulant matrix created from this image contains all possible translations of the image along its dimension:

As you may have noticed, this matrix contains a lot of redundant data but we need to know only the first row to actually generate the matrix. But these matrices also have a really amazing mathematical property: they are all made diagonal by the Discrete Fourier Transform (DFT), regardless of the generating vector! So, by working in the Fourier domain we can avoid the expensive computation of matrix multiplications because all these matrices are diagonal and all operations can be done element-wise on their diagonal elements.

Using these nice properties, we can reduce the computational cost from to nearly linear , bounded by the DFT. The complexity comes from the Ridge regression formula that we need to solve to learn a representation of the target:

In other words, the goal of training is to find a function that minimizes the square error over samples (which are the rows of the matrix X in the 1D example) and their regression targets . This means finding the parameters .

There is still one last step which we can do to improve the algorithm. That is we can use the “kernel trick” to allow more powerful non-linear regression functions . This means moving the problem to a different set of variables (the dual space) where the optimization problem is still linear. This usually also means on the downside that evaluating typically grows in complexity with the number of samples. But we can use again all the properties previously discussed to the kernelized version of Ridge Regression and obtain non-linear filters that are as fast as linear correlation filters, both to train and evaluate. All the steps are described in more detail in the original paper [1].

Results

Again, every step described up to now can be easily generalized to three dimensional volumes, same as Medianflow. As soon as I completed the generalization, I tested the algorithm first on the dummy data and the results were almost instantaneous… but wrong. But not for long, I just needed to adjust just some parameters! And the speed was still quite impressive. So it was time to test it on real world data.

This data comes from the tomographic reconstruction of a system that is a constriction through which a liquid foam is flowing. It was collected from one of Europe’s several synchrotron facilities (big X-ray machines). In general, tracing the movements can allow us to better understand some properties of the material and it has several application both in industry (i.e. manufacturing or food production)  and academic research experiments. Unfortunately, as of this time I only have three frames available. You can see a rendering of the data just below.

Rendered animation of the flowing foam system.

It’s easy to see why this is a high performance computing problem, look at all those bubbles! But this is not the only reason! These 3D volumes are represented through voxels (the 3D version of pixels in a 2D image) and while you can’t see it in the rendering animation, they keep the full information about depth of the data. (If you think of pixels as pieces of a cardboard puzzle, voxels would be like LEGO, which by the way are originally from here in Denmark!). This is why they can take so much disk space, each frame taking up to 15 GB. The algorithm is generalized to these sequences of 3D volumes and designed to work directly on the voxels. But now, without further ado, here’s the results of the tracking for a bubble:

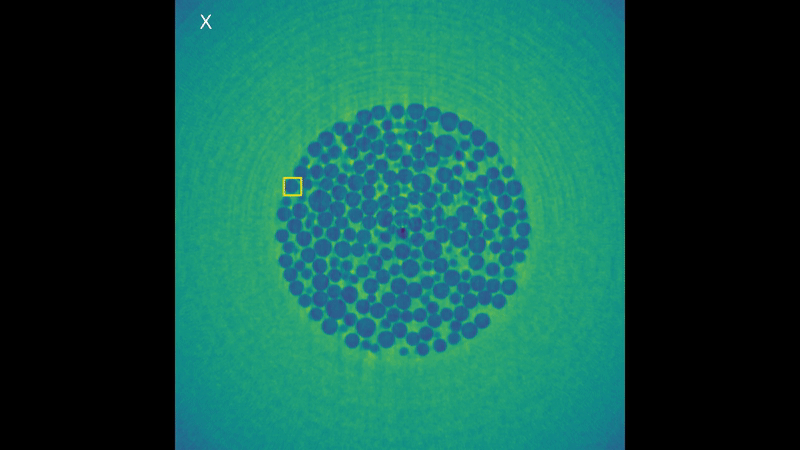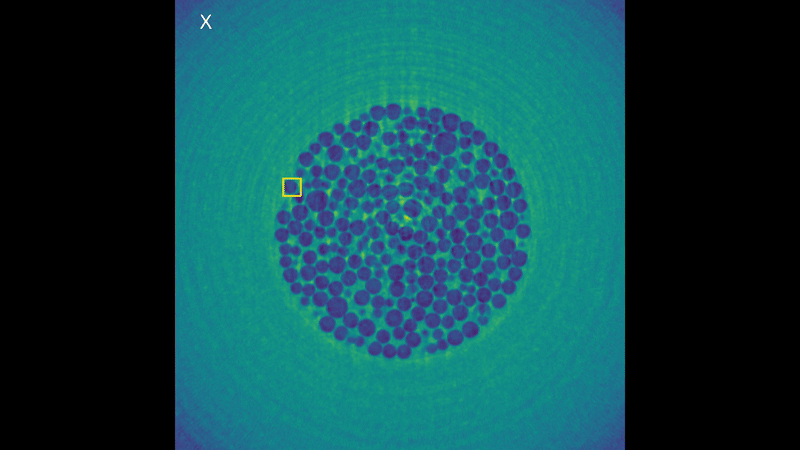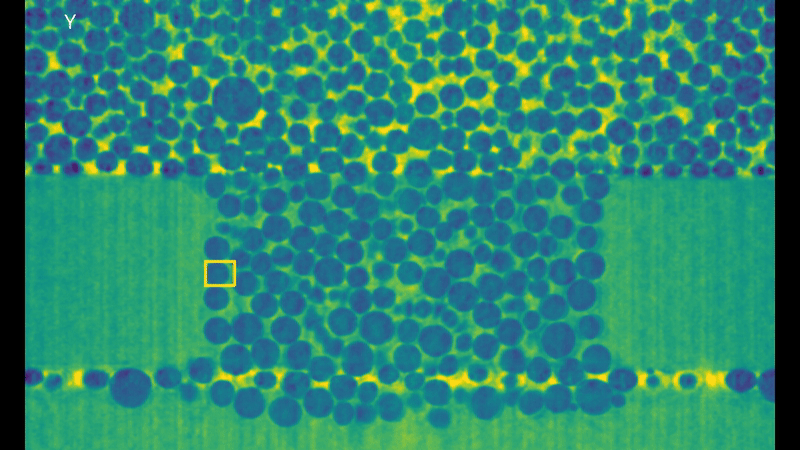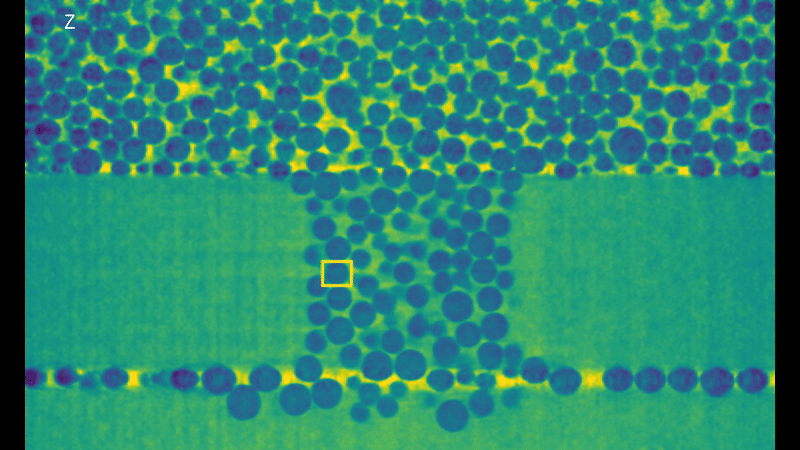
Visualization of the tracking results of KCF in each dimension.

It works! And it takes only about 15 seconds per frame for one bubble. That’s a x100 speedup compared to Medianflow! While these results look very promising, there is still a lot of work to do. First of all, we need further testing of the algorithm with different kinds of real data. (As I had limited options for this during the summer, I spent more time than I care to admit to create some voxel art animations and test the algorithms on those… you can check the results in the video presentation at the top of the page). Then, we still need to implement it in a true high performance computing fashion and make a version of the algorithm that can run on multiple nodes in a cluster. For now, the algorithm runs only on a single node, but it’s possible to speed up the computation by using a GPU for the Fourier transform. Only then my project will be truly done. But the summer is almost over and I need to come back home, hopefully I will have another chance to keep working on it!

References