Can this WORK??? check out!

Greetings everyone!

Welcome to my second post about my experience with Summer of High Performance Computing. First of all I hope that you are doing well and you had an enjoyable summer. If you haven’t already, go check my previews post, so you can get to know me a little better.

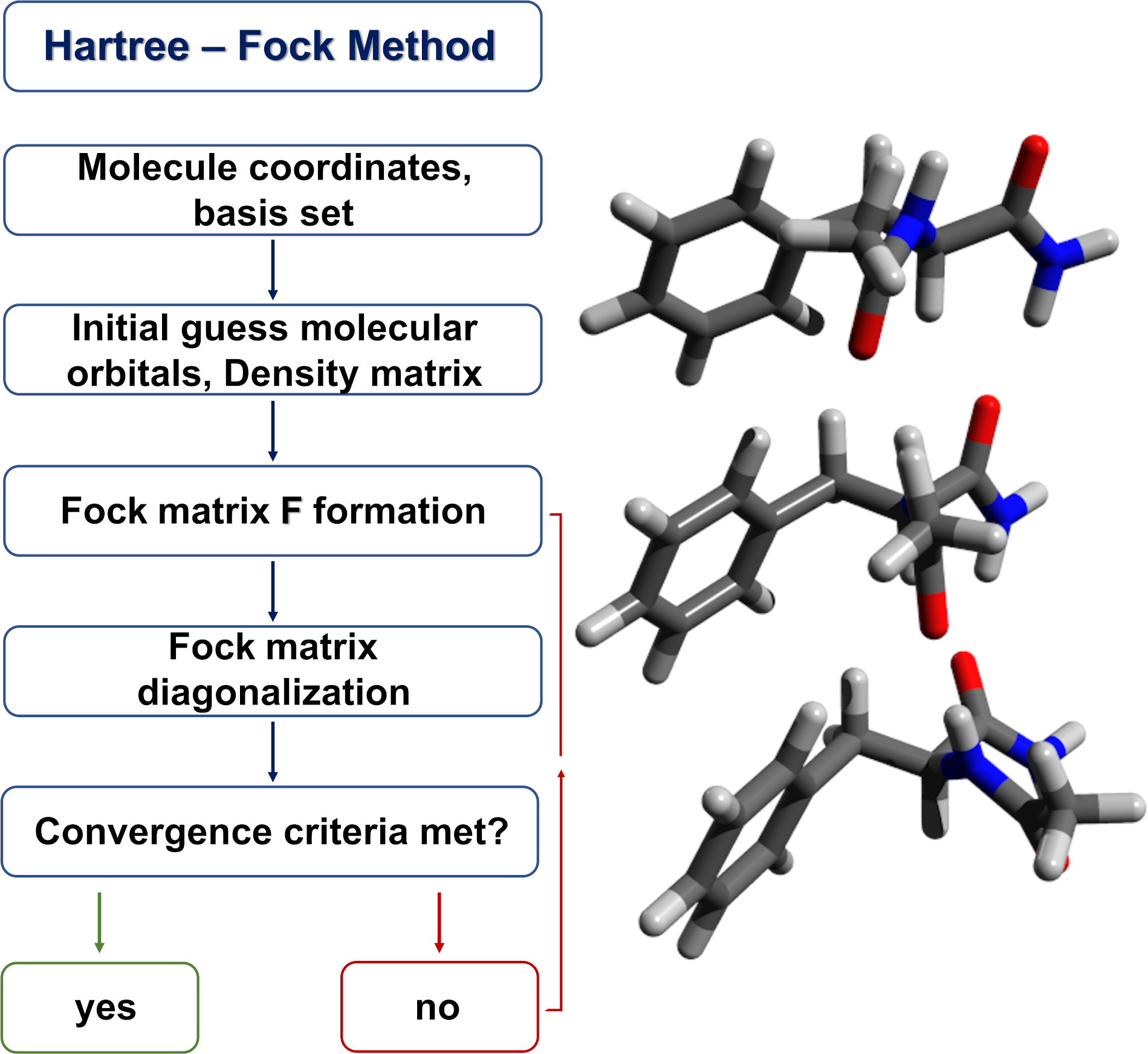
As I mention on my previous post, this summer I was working together with Eduard Zsurka under RNDr. Ján Simunek guidance, in order to implement and test a BLAS (Basic Linear Algebra Subprograms) version written in Fortran, to an existing code of Hartree-Fock algorithm written by Ján Simunek et al. What is Hartree-Fock you may ask. Simply put Hartree-Fock is a method that it can give us an approximation for the determination of the wave function and energy of a quantum N-body system in its ground state. Even simplier put, what this method does is to do an approximation solution of Schrödinger equation.

In this method there are two time consuming steps in the algorithm. One is the formation of Fock matrix which is a approximation through iterations to the single-electron energy operator for a given basis set and derives from integrals and density matrix. The second step is the diagonalization of the Fock matrix, which for linearly scaling methods and parallelization is an unwanted step. Dr Simunek et al. managed to replace the diagonalization step by replacing it with matrix-matrix multiplications. For larger molecules the electron integral matrices are sparse. Sparse matrices have the advantage that only the non-zero elements need to been stored and thus the matrices are occupying less memory.

Our task was to find libraries that can handle sparse matrix multiplications written in Fortran. The first two candidates where two libraries, one from National Institute of Standards and Technology (NIST) and the second one from netlib. With both of these libraries we had difficulty to successfully implement them to existing code, because of lacking documentation or not compiling with newer versions of Fortran. By that time we were searching for another way to implement from those libraries a sparse matrix-matrix multiplication or even to use intel’s Sparse BLAS library, we found a stackoverflow post with a guide for a working implemantation of netlib’s library.

After we managed to have a working test code from the said library we tested to methane molecule, where we found that our test code was working. Succeeding that we started testing the code on methotrexate (C₂₀H₂₂N₈O₅), and 5 different alkanes: C₆H₁₄, C₁₂H₂₆,  C₁₈H₃₈,  C₂₄H₅₀, C₃₀H₆₂, C₃₆H₇₄. Starting with methotrexate the results weren’t that great since our code was actually slower than the original code. These results didn’t disappoint us at all since we knew we had to go for bigger molecules, where we have even bigger sparse matrices.

This is the end of this post. We managed to have a working code and we are looking forward for more results. In my next post, we are going to see if for bigger molecules we can decrease the running time of the code. Thank you for reading my post.