High performance summer – A new code

In a repository far, far away, Stan is being developed.
The struggle for efficient sampling
“It is a period of computational war. Random walkers, striking from an initial position, have sampled from probability distributions and computed their first expectation against the continuous Random Variable. During the sampling, the Statistical Community managed to steal secret measure-theoretic descriptions of the Distribution’s ultimate core, the typical set, a singular portion of spaces with enough density-volume tension to compute an entire expectation.
Plagued by the Curse of Dimensionality, Morten and I race home aboard HPC, to implement the secret code that can save our fellow data scientists’ time and resources and sample efficiently in the galaxy.”

Welcome back! Last time I left you with a general introduction to the project and HPC. Now let us dive into some details!
Stan and MCMC
Stan’s a framework “for statistical modeling and high-performance statistical computation”, as the official page states, and is used extensively by statisticians and scientists. Among other things, it offers algorithms for Bayesian statistical inference: it is the use of data analysis for determining the properties and the parameters of a probability distribution, using the Bayes’ theorem. Now, if the probabilistic model can be expressed as a graph, where a node represents a random variable (RV) and an edge the conditional dependence between RVs, then we can use simulation algorithms, like Markov Chain Monte Carlo (MCMC) methods. The idea is pretty simple: these algorithms sample from RVs, using those samples to compute integrals over that RV, such as expectation or variance. How do they sample? An ensemble of random walkers wanders around the space, applying the so-called Markov transitions and trying to obtain samples that will contribute significantly to the integral.

As you may imagine, lots of MCMC algorithms exist, with their ups and – especially – downs. Simplifying a bit, they can waste a lot of computational resources (and time!) sampling from regions that are irrelevant for computing those integrals: the integrals make use of both the distribution and the volume, and it turns out that, while the former is mostly found near the mode, the latter quickly accumulates away from it. Only a very narrow region, more and mo\re singular as the dimension grows, contributes to the integral: the typical set. How to reach and explore it? An ingenious method called Hamiltonian Monte Carlo (HMC) has been devised that simulates Hamiltonian dynamics, treats samples like physical particles, and exploits the symplectic properties of the Hamiltonian flux to approach and explore the typical set efficiently.
Wanting a better HMC
Now, Stan offers some great MCMC algorithms, and HMC is among them. Our job for this project consisted in implementing a yet more efficient version of the HMC and, if possible, parallelise it!
One thing about HMC is that it doubles the space dimension and has two variables to handle: a position and a momentum. The momentum allows a particle (~ sample) to follow the field lines and us to exploit the gradient of the distribution to direct it properly. How, you may ask? As with any numerical simulation, we need to integrate the orbit, and do so with the symplectic integrators, which have the nice property of volume preservation: this means that the computed path cannot deviate too much from the actual path, even for long integration times. Symplectic integrators can be derived from the Hamilton equations and can be of any order k; the simplest ones being:
- k = 1: symplectic Euler
- k = 2: Störmer-Verlet, with variations (such as the leap-frog, which we used!)
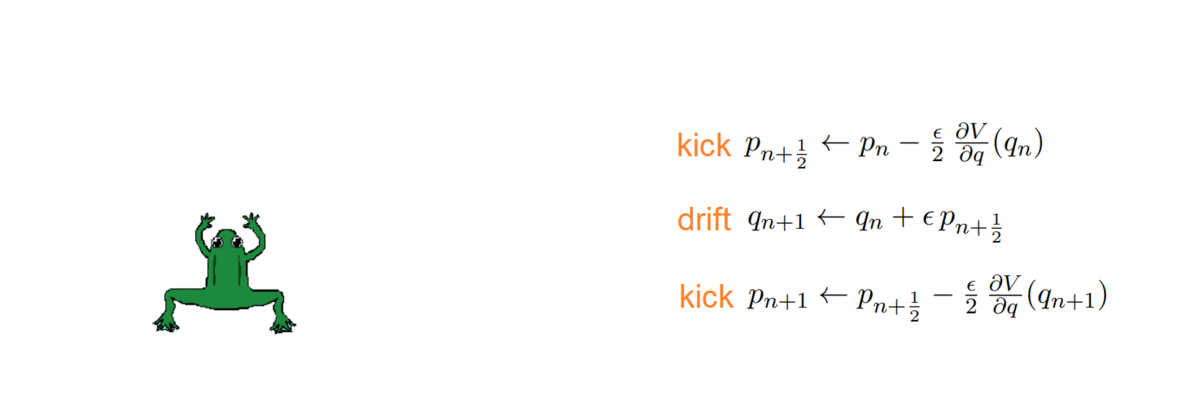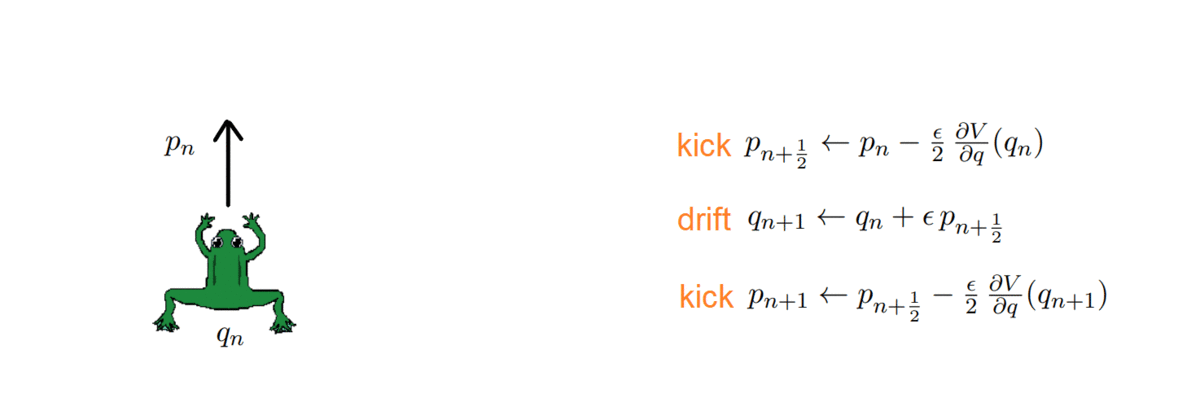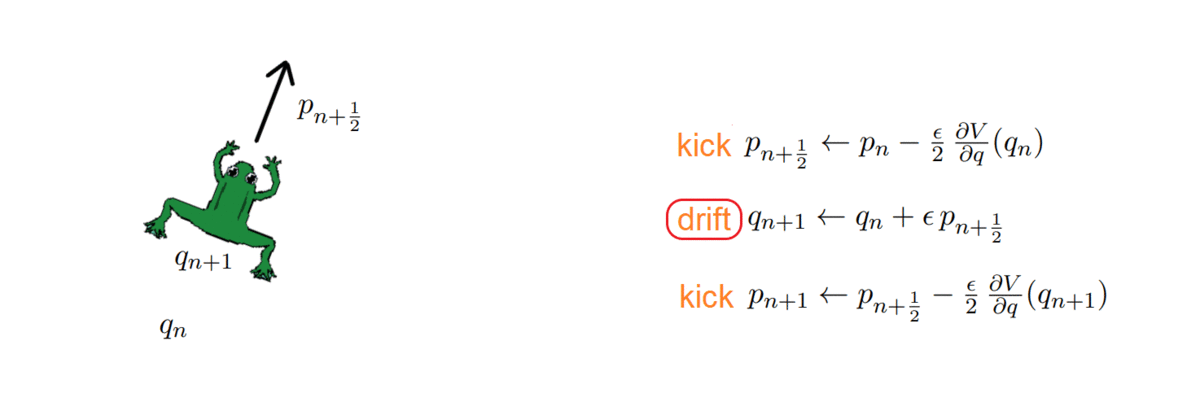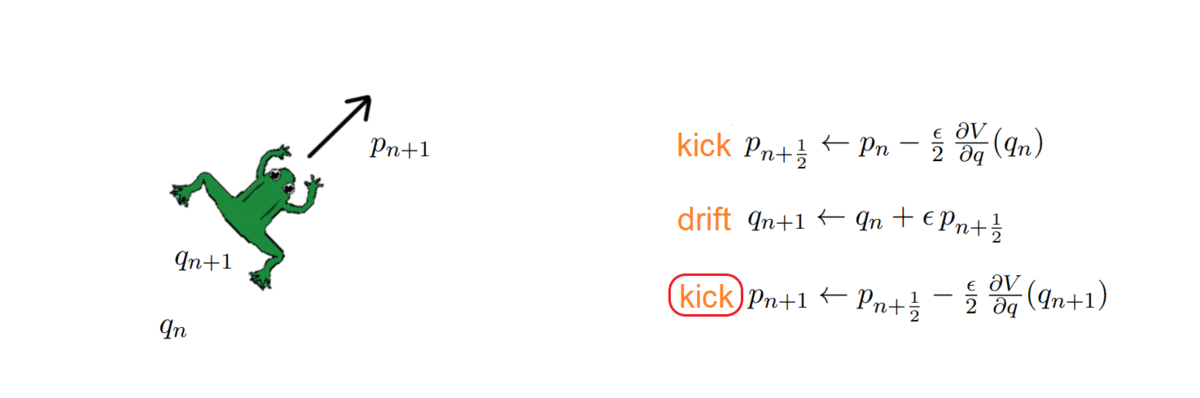
The HMC, after every integration, obtains a proposal and decides whether to accept or reject it, i.e. to keep it as a new sample or ignore it. To do so, it computes the total energy (or Hamiltonian) of the system before and after integrating: samples whose energy has reduced in the process are accepted unconditionally, while the others are exponentially more likely to be rejected.
Building a better HMC
We were given a very complex C++ code skeleton to be completed and/or reformatted; this code could be submitted to the Stan Framework. The way we proceeded is as follows:
- we implemented a data structure using the Structure of Array (SoA) model: the ensemble of particles holds one array for each particle’s feature (so 2 arrays in our case: positions and momenta);
- we completed the integrator structure, devising how the integration should be performed: namely, with the afore-mentioned leapfrog;
- we added functionalities to another script for the actual computations: in there, the algorithm samples, computes the Hamiltonian, and decides if to accept or reject the proposals; finally, it estimates the parameter of the input model (after all, we’re performing what is called stochastic parameter fitting).
We are pretty satisfied with our implementation since it’s fast and produces meaningful results. Still, there’s a world to be explored!
Beyond HMC
For example: when implementing the integration, we had to specify a step size and a number of steps, since these are not automatically computed by the algorithm. We have also experimented with a 3° order “Ruth” integrator, which turned out fast (and required a larger step size and a smaller number of steps). There is a variant of the HMC algorithm, the No-U-Turn Sampler (NUTS), which eliminates the need for setting the number of steps (and offers some heuristics for computing a good step size).
But that’s for another time! Thanks for your attention.
