Computation of the volume of molecules
Hello again to my third blog post!
Today I want to tell you what I was working on the last few weeks. As I have mentioned in my previous blog post (https://summerofhpc.prace-ri.eu/how-to-distinguish-different-surfaces-of-molecules/), one goal of this year’s project is to distinguish different disconnected surfaces automatically. It can happen that the computation yields several very small surface components which are physically irrelevant. For example, in the image above we see one large surface (grey), and several tiny surface components inside of the large surface. The goal is to sort out these small surfaces automatically. For doing that we need a criterium when a surface should be sorted out and when not. The approach that we used in our implementation is the computation of the volume of each single surface component. If the volume falls off a certain threshold value, the corresponding surface can be sorted out.
In this blog post, I want to describe how we computed the volume of a molecule. The divergence theorem, also known as the Gauss-Ostrogradsky theorem (https://mathworld.wolfram.com/DivergenceTheorem.html), gives us a formula for doing this.
Let S be the surface of a molecule. Then, the theorem leads to the following formula:
Volume of the molecule =
Here, for each point (x,y,z) on S, \vec{N} is the unit normal pointing outwards of the surface S at (x,y,z). To use this formula for our computations, we approximate the integral by a finite sum:
Volume of the molecule
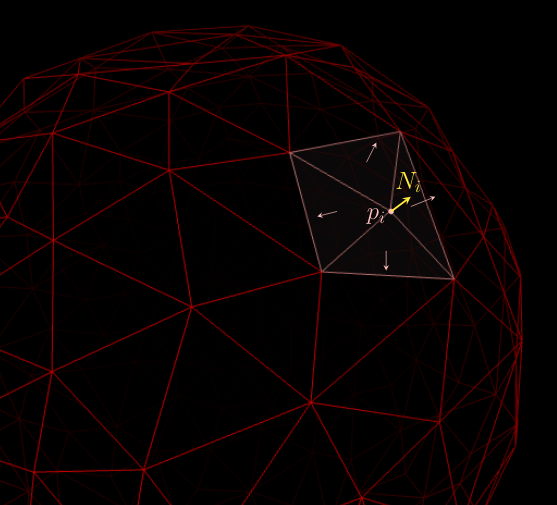
Our program computes a triangulation that approximates the surface of a molecule. Each 
(yellow) is the average of the triangle normals (pink) of those triangles that contain the vertex In our program, for each disconnected surface, we compute its volume. As a threshold value, we chose the volume of a 
This was a rough overview of the computation of the volumes. If you are interested in more details, feel free to ask your questions in the comments below.
Leave a Reply