How to distinguish different surfaces of molecules?
Hello again to the second blog post!
During the summer we (me and Ulaş Mezin) are working on the Implementation of Molecular Surfaces (https://summerofhpc.prace-ri.eu/hpc-implementation-of-molecular-surfaces/). In this blog post, I want to describe to you what I was working on the last few weeks.
Last year, a first program has already been implemented. This program computes a triangulation that approximates the surface of a molecule. This year we are focusing on improving efficiency and adding new features. One of these new features I will present to you now:

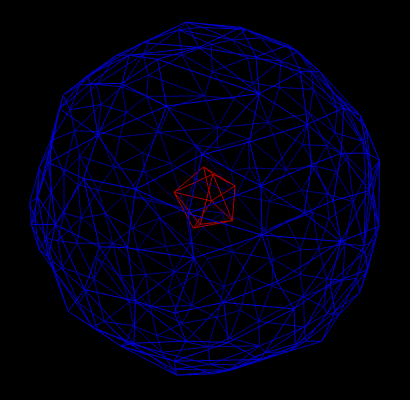
It may happen that the result of the computation yields several disconnected surfaces (see figure 1). However, in applications, one is often only interested in the outer surface. If we look at the picture, it is easy for us humans, to say which triangle on the triangulation belongs to which surface. However, for a computer, it isn’t as easy as it might seem at first sight. For applications, it is important to distinguish different connected surfaces automatically. Therefore, we need an algorithm to tackle this problem (and this algorithm should be ideally efficient).
For the computer, the computed triangulation of the program is just a bunch of triangles. An example, how a triangulation looks like, is depicted in figure 2. The computer has knowledge of local connectivity in the sense that the vertices of a single triangle are connected to each other and must therefore lie on the same surface. But if we look at two arbitrarily chosen vertices of the triangulation (for example vertex 1 and vertex 9 in figure 2) it is not apparent if these two vertices lie on the same surface or not, by looking only at the list of triangles and vertices which are stored in memory. But can the computer combine the local knowledge to obtain global information about the surfaces? And if so, how is this done most efficiently?

Triangulation stored in Computer 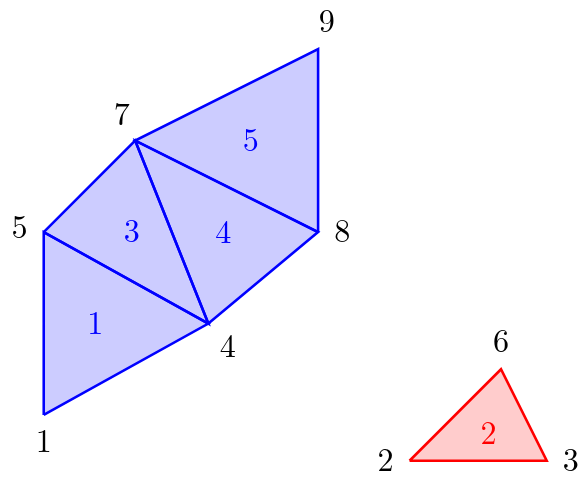
Visualised Triangulation
One solution to this problem is to use the Disjoint-set data structure (also know as Union-find data structure or merge-find set, for more details see https://en.wikipedia.org/wiki/Disjoint-set_data_structure). This data structure stores a collection of non-overlapping sets. In our case, each set consists of all vertices of one connected surface. If we look again to figure 2, we would have the sets {1, 4, 5, 7, 8, 9} and {2, 3, 6}.
In our program, the disjoint-set structure is implemented with a so-called “disjoint-set forest”. A forest is a set of trees (see figure 3). In our algorithm, we start with an “empty” forest (i.e. we have no trees at all). By going through the list of triangles sequentially, the trees are constructed little by little. If you are interested in more details I can recommend reading https://www.geeksforgeeks.org/disjoint-set-data-structures/ and http://cs.haifa.ac.il/~gordon/voxel-sweep.pdf. In our example from figure 2, the resulting forest consists of two trees. Each tree contains the vertices of one surface. As soon as we have constructed those trees, distinguishing different surfaces is relatively easy. If we look at a vertex on the surface, we can traverse up the corresponding tree up to the root vertex. If two vertices lie on the same surface, the corresponding root vertices match. Conversely, if the vertices do not lie on the same surface, the corresponding root vertices are different.

I hope you enjoyed reading this blog post. Describing all the details of how the algorithms works would blow up the length of this post, but if you are interested in further details you are welcome to ask questions in the comments section.
