Enter the Metric

In this article, we will have a look at performance improvements on a very basic level. A program can be written in many different ways, (hopefully) always obtaining the same result. Still, the execution time may differ drastically. In higher languages like Python, one may not tell instantly, how a predefined function is implemented. We will discuss this issue on the basis of the square function.

As my college Antonis mentioned in his article To Py or not to Py?, we are optimising a python CFD program. For increasing the performance of a program, one does not always need to switch to parallel methods. One can start with simple things, like choosing the right implementation of a function. An important function of this project is the distance function. It is used to quantify the difference between the two matrices. It is used to stop the iterative process when the output is merely changing and therefore a minimum is reached.

The distance function uses the Euclidian metric . It calculates a scalar from the equally sized matrices and . This function provides a lot of parts to investigate. In this article, we will only look at the . You can investigate the rest of the function at home with the techniques provided.

To start we generate a random matrix of the size

import numpy
A = numpy.random.rand(m)

The square can be now computed using a for-loop

for i in range(m):
A[i]*A[i]

or the numpy.power-function

numpy.power(A,2)

or the python power function

A**2

or a multiplication

A*A

to just name a few. In IPython a code snippet can be easily timed with

%timeit [expression]

I wrote a script to time the previous functions for different sizes of , using the time-library. In the figure, the execution times of those implementations for different sizes of A are compared.

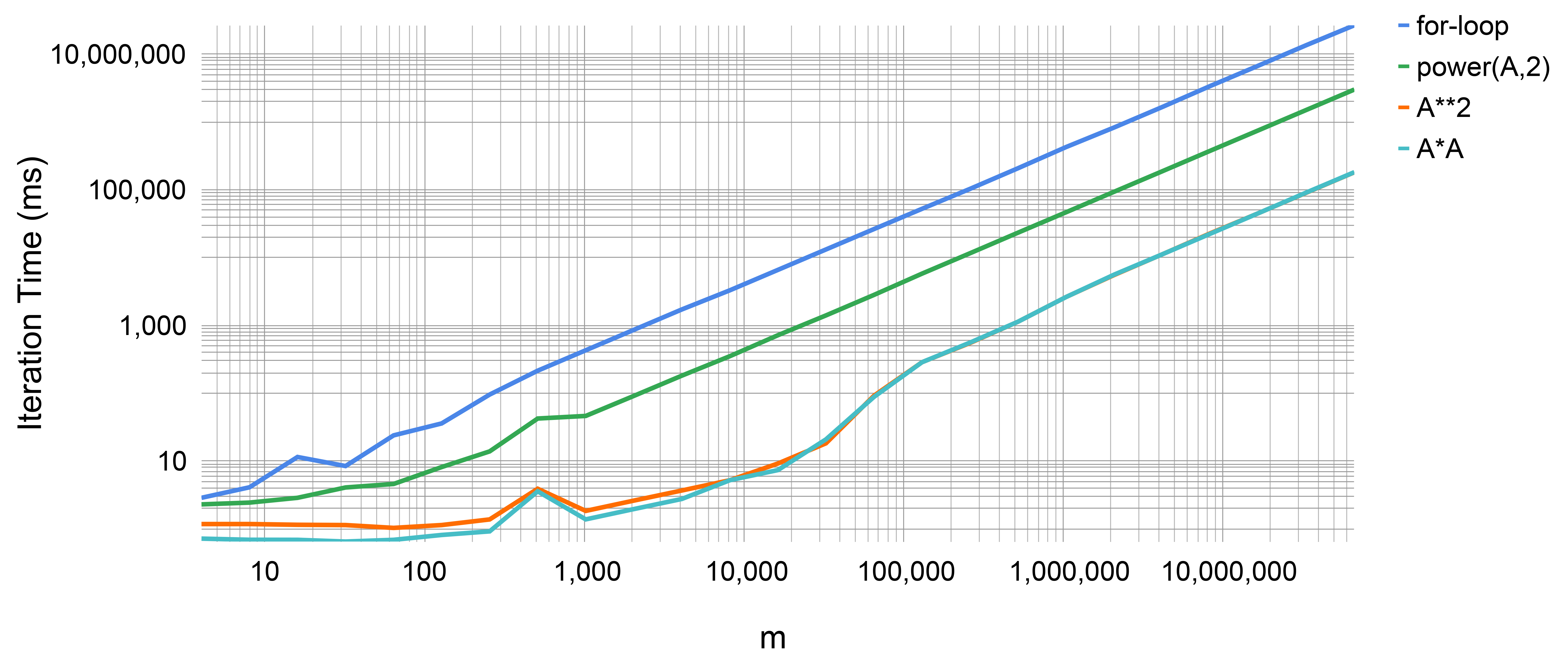
Unsurprisingly the for-loop is rather slow. The simple multiplication may be up to one-hundred times faster. The numpy.power function is somewhere between. This may be more of a surprise. The numpy.power-function may be written especially for NumPy arrays. Of course, it provides more options and IS faster for larger exponents >70. For simple expressions like the square, an inline implementation should be chosen.