Putting it all together – simulating irradiation damage and computing thermal conductivity

As I explained both the methods used as well as the field of application of my project in my last two blog posts, I now want to gather all the information and finally describe which simulations were carried out by my colleague Arda Erbasan and me.
Setup
How to calculate thermal conductivity using molecular dynamics?
Using the definition of Wikipedia: The thermal conductivity of a material is a measure of its ability to conduct heat. For a given material it can be computed with the aid of Fourier’s law q = -kappa ⋅ ∇T where q is is the heat flux and ∇T describes a spatial temperature gradient. Thus knowing q and ∇T enables us to calculate the thermal conductivity kappa. One possible way of doing so, is to define two distinct regions in the simulation box and add/subtract the same amount of energy to/from the two regions respectively establishing a known heat flux q and a temperature gradient ∇T between the resulting hot and cold region[1,2].
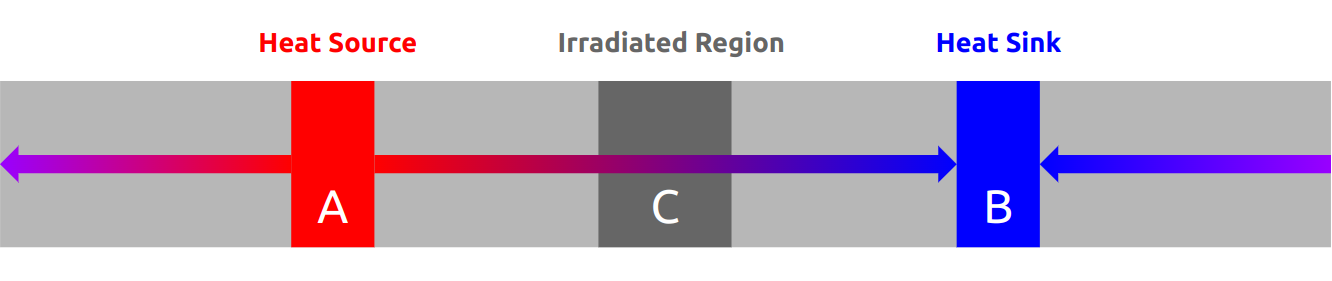
In our specific case we created a simulation box of cuboid shape and dimensions of ~ 158 x 15.8 x 15.8 nm consisting of 2.5 Million (!) individual atoms. A region (labeled ‘A’ and ‘B’ in the sketch) was defined at one quarter as well as at three quarters of the total length. Right in the middle between these two regions, another distinct region (labeled ‘C’) was defined. Here, the thermal conductivity is calculated later. Before the temperature gradient is established, defects, as caused by high irradiation, are created in region ‘C’. For this purpose, a method is used which I will describe shortly.
Furthermore, the entire system is now heated in several stages to a desired target temperature. Only then, energy is added/subtracted from regions ‘A’ and ‘B’ respectively and thus the difference in temperature is generated. Since we are using periodic boundary conditions, a second heat flux will also form, going through the boundaries of the simulation box. However, due to the symmetry of the system, this is accounted for by dividing the heat flux q by a factor of 2.
How to simulate radiation damage using molecular dynamics?
Since we are interested in the thermal conductivity of irradiated tungsten, we use an algorithm called “creation-relaxation algorithm” – CRA[3] for short – to simulate radiation damage inside the metal at relatively low computational cost. In it’s essence, this method first displaces a random atom in the crystal to a new random position and then minimizes the energy of the new configuration (relaxation step) thus introducing pairs of vacancies and interstitial atoms – also called “Frenkel pairs”. This procedure is repeated until a desired level of damage is reached – as measured by the amount of displaced atoms. As mentioned before, the system undergoes a heating procedure after damage is created but before the thermal conductivity is measured. During this thermalization procedure, some of the created Frenkel pairs recombine and thus vanish.
The image below shows examples of said defects. Red are interstitial atoms, forming extended defect clusters and blue are vacancies. The green and pink lines indicate dislocation loops, a special type of defect structure, about which I will not explain in detail here.

Results
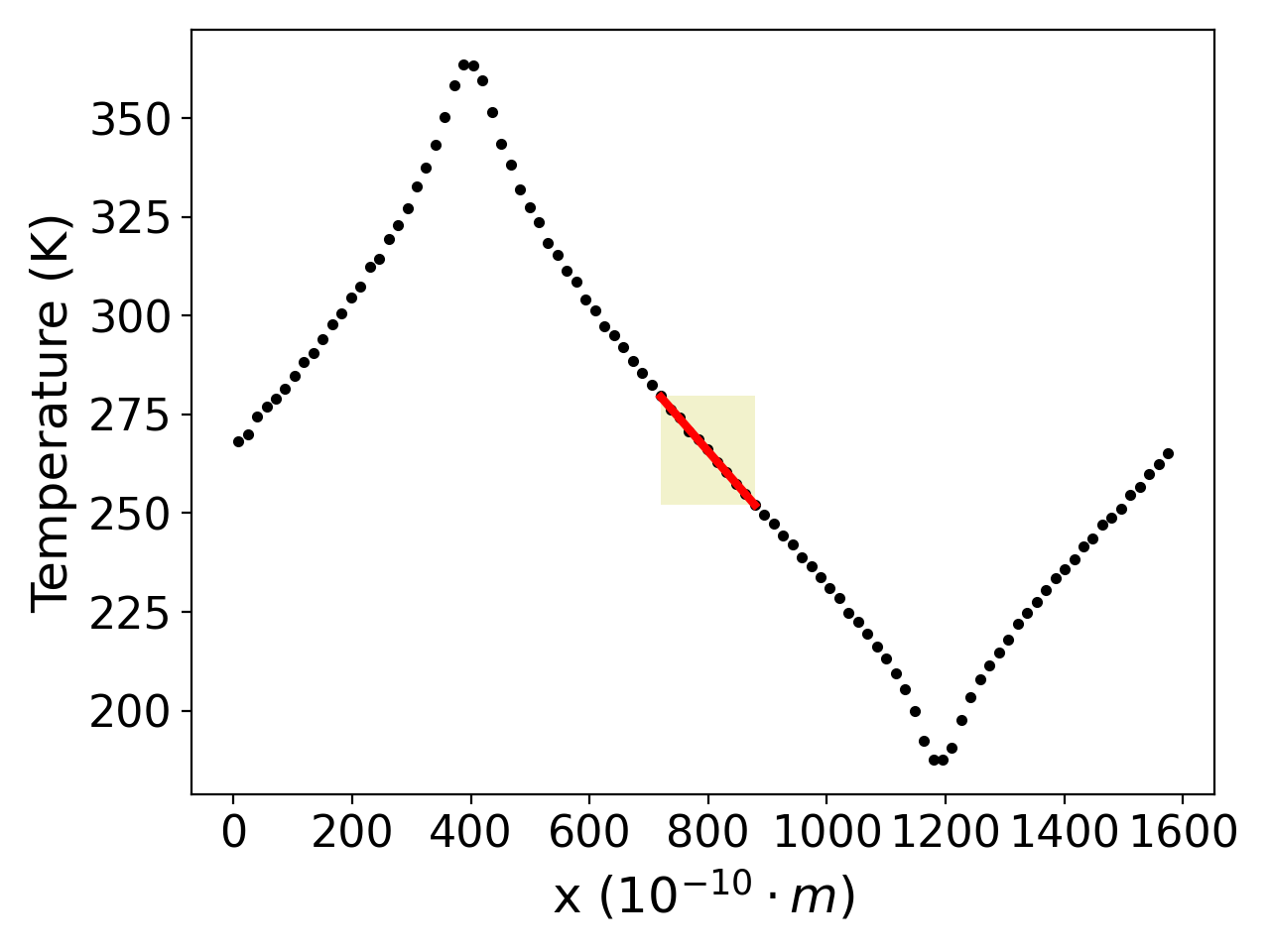
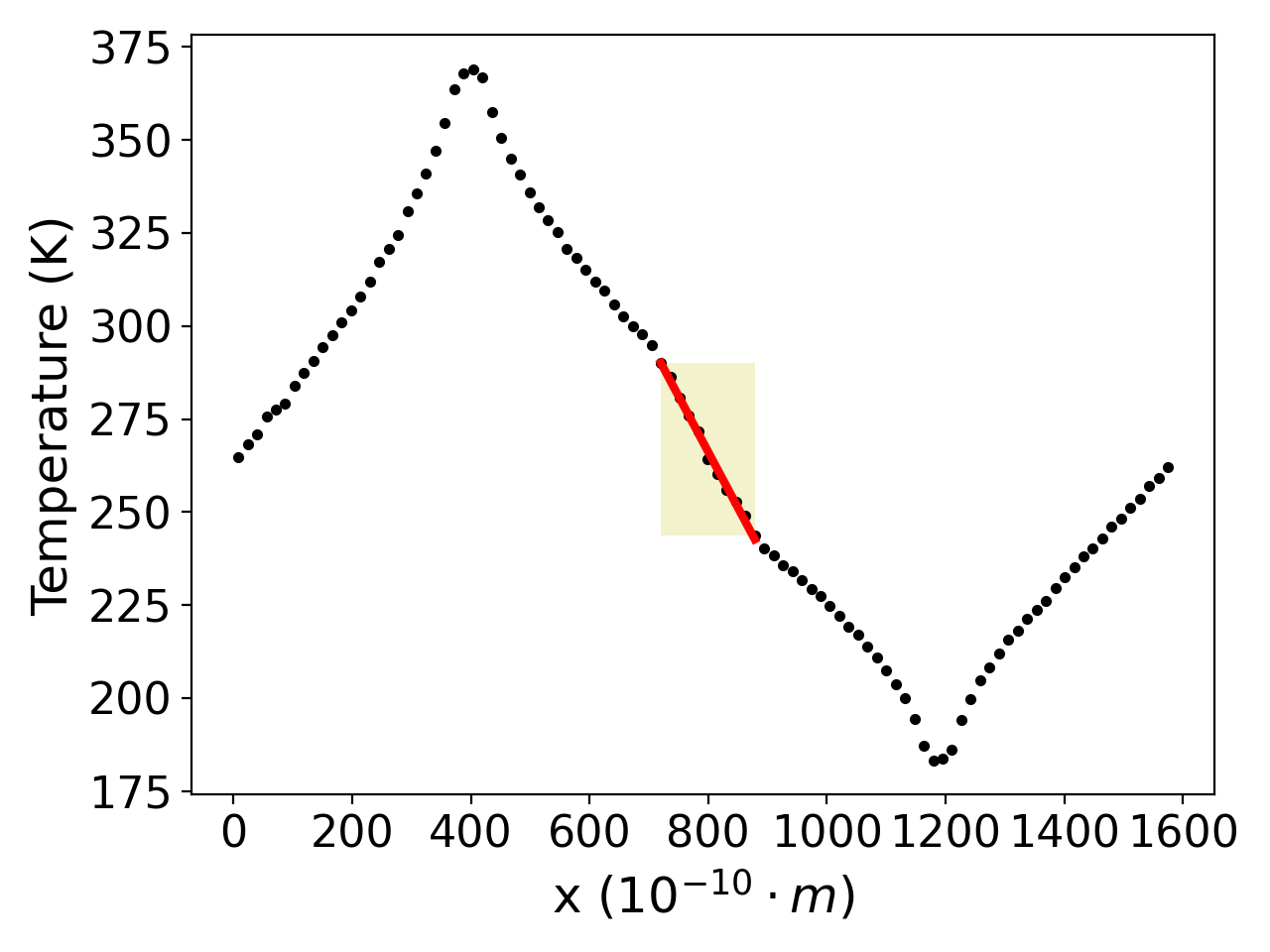
The following plots display the temperature profile of an undamaged system on the left and a damaged system – with 1038 final defects after recombination – on the right, both at a temperature of 300 K. The temperature profile was computed in the direction of the imposed heat flux.
The interesting part for us is located in the middle, which corresponds to the middle 10% of the system as described on the previous slide. In the undamaged system, we observe a smooth temperature gradient from the hot to the cold region. In contrast, in the damaged system, a clear change in the slope of the temperature gradient can be seen. This indicates poorer thermal conductivity: The perfect system exhibits a thermal conductivity of 18.59 Watts per Meter-Kelvin while the damaged system has a thermal conductivity of only 10.7 Watts per Meter-Kelvin.
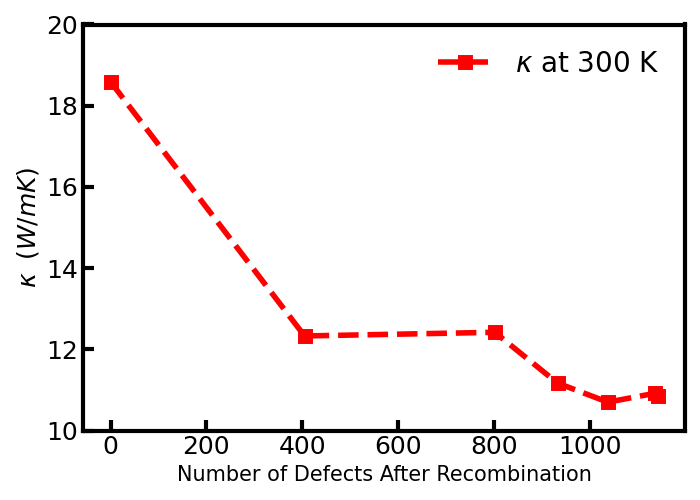
To better quantify this behavior, we analyzed the trend in thermal conductivity with respect to the overall damage of the system as measured by the final number of defects. As can be seen, an increase in the number of defects comes with a decrease of thermal conductivity. We also observed some deviations from the main trend – possibly due to the statistical nature of the simulations.
A few remarks on computational effort
Using 10 compute nodes of MareNostrum4 each one equipped with 2 sockets Intel Xeon Platinum 8160 CPU with 24 cores each @ 2.10GHz the whole simulation of a 2.5 Million atom system for a total of over 1 Million time steps was completed in less than 3 hours.
Conclusion
To wrap up, using this simulation setup we were able to observe a decrease in thermal conductivity of irradiated tungsten as compared to a perfect tungsten system. Although further tests would be beneficial, not least to counteract the statistical nature of this method and to make more robust statements, these results are already very interesting as they clearly show how certain properties of tungsten, in this case the thermal conductivity, change under radiation load in a fusion reactor. This must, of course, be taken into account in the construction of future reactors and especially in the service life of wall elements and plasma-facing components. In this sense, the molecular dynamics simulations can be a first step towards a full-scale simulation of a fusion reactor.
References:
[1] Ikeshoji and Hafskjold, Molecular Physics, 81, 251-261 (1994).
[2] Wirnsberger, Frenkel, and Dellago, J Chem Phys, 143, 124104 (2015).
[3] P. M. Derlet and S. L. Dudarev, PHYSICAL REVIEW MATERIALS 4, 023605 (2020).