Read this if you want your computer to run your applications faster [Difficulty: Easy]
![Read this if you want your computer to run your applications faster [Difficulty: Easy]](https://summerofhpc.prace-ri.eu/wp-content/uploads/2019/08/john-jemison-GS-ArbPX56Y-unsplash.jpg)
[Video] Hi from Dublin everybody! Welcome back to my blog or welcome for newcomers.
If you have missed it, my previous blog post is available here! No worries, there is no need to read it before this one to understand today’s topic. You can read it after to know more about me if you want, but follow and stay tuned until the end of this post because I have a special announcement for you to do!
Before explaining how you can make your computer run your applications faster, I just wanted to come back quickly to our training week in Bologna, Italy, and make a point with you on my current situation.
Training week summary
As a picture is worth a thousand words, I let you discover by images the summary of this amazing training week.
Where am I now?
Since the 6th of July, I am in Dublin with Igor, another PRACE SoHPC 2019 student. We are both working on our projects at ICHEC (Irish Centre for High-End Computing), an HPC Center. Paddy Ó Conbhuí (my super project mentor at ICHEC) and I are dealing with a parallel sorting algorithm: the parallel Radix Sort, which is my project.
Enough digressions, you are most probably here to read about application and computer speed.
Pursuit of speedup
To make our applications and programs run faster, we have to find first where, in our programs, computers spend most of the execution time. Then we have to understand why and finally, we can figure out a solution to improve that. This is how HPC works.
- Identify the most time-consuming part of a program
- Understand why it is
- Fix it / Optimize it
- Iterate this process again with the new solution until to be satisfied with the performance
Let’s apply this concept to a real-world example: how can we find a way to improve programs in general? Not a specific algorithm or program but most of them in a general way? It is an open and very general question with a couple of possible answers, but we will focus on one way: optimize sorting algorithms. We are going to see why.
How do computers spend their time?
We have to start by asking what takes time and can be improved in computer applications. Everything starts with an observation:
“Computer manufacturers of the 1960’s estimated that more than 25 percent of the running time of their computers was spent on sorting, when all their customers were taken into account. In fact, there were many installations in which the task of sorting was responsible for more than half of the computing time.”
From Donald E. Knuth’s book Sorting and Searching
In 2011, John D. Cook, PhD added:
“Computing has changed since the 1960’s, but not so much that sorting has gone from being extraordinarily important to unimportant.”
From John D. Cook, PhD in 2011
Why this still might be true nowadays?
It is become rare to work with data without having to sort them in any way. On top of that, we are now in the era of Big Data which means we collect and deal with more and more data from daily life. More and more data to sort. Plus, sorting algorithms are useful to plenty more complex algorithms like searching algorithms. On websites or software, we always sort products or data by either date or price or weight or whatever. It is a super frequent operation. Thus, it is probably still true that your computer spends more than a quarter of its using time to sort numbers and data. If you are a computer scientist, just think about it, how often did you have to deal with sorting algorithms. Either wrote one or used one or used libraries which use sorting algorithms behind the scene. Now the next question is what kind of improvement can be done regarding sorting algorithms? This is where the Radix Sort and my project come into play.
Presentation of the Radix Sort
It has been proved that for a comparison based sort, (where nothing is assumed about the data to sort except that they can be compared two by two), the complexity lower bound is O( N log(N) ). This means that you can’t write a sorting algorithm which both compares the data to sort them and has a complexity better than O( N log(N) ). You can find the proof here.
The Radix Sort is a non-comparison based sorting algorithm that can runs in O(N). This maybe sounds strange because we often compare numbers two by two to sort them, but Radix Sort allows us to sort without comparing the data to sort.
You are probably wondering how and why Radix Sort can help us to improve computer sorting from a time-consuming point of view. We will see it after explaining how does it work and go through some examples.
How does Radix Sort work?
Radix sort takes in a list of N integers which are in base b (the radix) and such that each number has d digits. For example, three digits are needed to represent decimal 255 in base 10. The same number needs two digits to be represented in base 16 (FF) and 8 in base 2 (1111 1111). If you are not familiar with numbers bases, find more information here.
Radix Sort algorithm:
Input: A (an array of numbers to sort) Output: A sorted 1. for each digit i where i varies from least significant digit to the most significant digit: 2. use Counting Sort or Bucket Sort to sort A according to the i’th digit
We first sort the elements based on the last digit (least significant digit) using Counting Sort or Bucket Sort. Then the result is again sorted by the second digit, continue this process for all digits until we reach the most significant digit, the last one.
Let’s see an example.
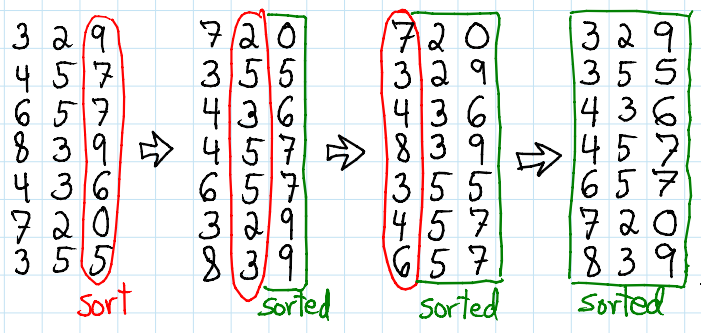
Source: https://brilliant.org/wiki/radix-sort/
In this example, d equals three and we are in base 10. What if all the numbers don’t have the same number of digits in the chosen base? It is not a problem, d will be the number of digits of the largest number in the list and we add zeros as digits at the beginning of other numbers in the list, until they all have d digits too. This works because it doesn’t change the value of the numbers, 00256 is the same as 256. An example follows.
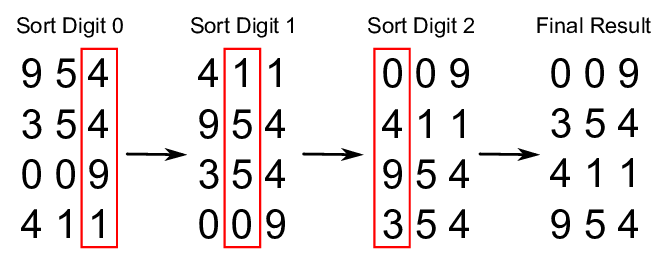
Source: https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/radix-sort
Keep in mind that we could have chosen any other number base and it will work too. In practice, to code Radix Sort, we often use base 256 to take advantage of the bitwise representation of the data in a computer. Indeed, a digit in base 256 corresponds to a byte. Integers and reals are stored on a fixed and known number of bytes and we can access each of them. So, no need to look for the largest number in the list to be sorted and arrange other numbers with zeros as explained. For instance, we can write a Radix Sort function which sorts int16_t (integers stored on two bytes) and we know in advance (while writing the sort function) that all the numbers will be composed of two base 256 digits. Plus, with templates-enable programming languages like C++, it is straightforward to make it works with all other integer sizes (int8_t, int32_t and int64_t) without duplicating the function for them. From now, we assume that we use the base 256.
Why use counting sort or bucket sort?
First, if you don’t know Counting Sort or Bucket Sort, I highly recommend to read about it and figure out how they work. They are simple and fast to understand but expose and explain them here will make this post too long and it is not really our purpose today. You will find plenty of examples, articles and videos about them on the internet. Sorting algorithms are at least as older as computer science and first computers. They have been studied a lot since the beginning of programmable devices. As a result, there is a lot of them and it is not only good but also important to know the main ones and when to use them. Counting and Bucket sorts are among the most known.
They are useful in the Radix Sort because we take advantage of knowing all the value range one byte can take. The value of one byte is between 0 and 255. And this helps us because in such conditions, Counting Sort and Bucket Sort are super simple and fast! They can run in O(N) when the length of the list is at least a bit greater than the maximum (in absolute value) of the list and especially when this maximum is known in advance. When it is not known in advance, it is more tricky to make the Bucket sort runs in O(N) than the Counting. However, in both cases, the maximum and its issues have to be managed dynamically. They can run in O(N) because they are not comparison-based sorting algorithms. In our case, we sort according to one byte so the maximum we can have is 255. If the length of the list is greater than 255, which is a very small length for an array, Counting and Bucket sorts in Radix Sort, can easily be written having O(N) complexity.
Why not use only either counting or bucket sort to sort the list all of a sudden? Because we will no longer have our assumption about the maximum as we are no longer sorting according to one byte. And in such conditions, the complexity of Counting sort is O(N+k) and Bucket sort can be worse depends on implementations. Here, k is the maximum number of the list in absolute value. In contrast, with Radix Sort, you will have in worst case O(8*N) which is O(N) and we will explain why. In other words, since Radix Sort iterates through bytes and always sorts according to the value of one byte, it is insensitive to the k parameter because we only care about the maximum value of one byte. Unlike both the Counting and Bucket sorts whose execution times are highly sensitive to the value of k, a parameter we rarely know in advance.
The last point of why we use them in Radix Sort is because they are stable sorts and Radix Sort entirely relies on stability. We need the previous iteration output in the stable sorted order to do the next one. No better way to try it by yourself quickly on a paper sheet with a non-stable sort to understand why. Actually, you can use any stable sorting algorithm with a complexity of O(N) instead of them. There is no interest in using one with a complexity of O(N log(N)) or higher because you will call it d times and in such a case, it is just worse than call it once with the entire numbers to sort them all of a sudden.
Complexity of Radix Sort
The complexity is O(N*d) because we simply call d times a sorting algorithm running in O(N). Nothing more. The common highest integer size in a computer is integer on 8 bytes. So assuming we are dealing with a list of integers like that, the complexity using Radix Sort is O(8*N). The complexity will be lower if we know that they are 4 or 2 bytes integers as d will equal 4 or 2 instead of 8.
LSD VS MSD Radix Sort
The algorithm described above is called LSD Radix Sort. Actually, there is another Radix Sort called MSD Radix Sort. The difference is:
- With the LSD, we sort the elements based on the Least Significant Digit (LSD) first, and then continue to the left until we reach the most significant digit
- With the MSD, we sort the elements based on the Most Significant Digit (MSD) first, and then continue to the rigth until we reach the least significant digit
The MSD Radix Sort implies few changes but the idea remains the same. It is a bit out of our scope for today so we will not go in further details, but it is good to know its existence. You can learn more about it here.
How can Radix Sort be useful to gain speedup?
The Radix Sort is not so often used whereas well implemented, it is the fastest sorting algorithm for long lists. When sorting short lists, almost any algorithm is sufficient, but as soon as there is enough data to sort, we should choose carefully which one to use. The potential time gain is not negligible. It is true that “enough” is quite vague, roughly, a length of 100 000 is already enough to feel a difference between an appropriate and an inappropriate sorting algorithm.
Currently, Quicksort is probably the most popular sorting algorithm. He is known to be fast enough in most of the cases, although its complexity is O(N log(N)). Remember that it is the lower bound for comparison-based algorithms and the Radix Sort has a complexity of O(N*d). Thus, Radix Sort is efficient than comparison sorting algorithm until the number of digits (d parameter) is less than log(N). This means the more your list is huge, the more you should probably use the Radix Sort. To be more precise, from a certain length, the Radix Sort will be more efficient. We know the Radix Sort since at least punch cards era and it can do much better. So why it is not so used in practice?
Typical sorting algorithms sort elements using pairwise comparisons to determine ordering, meaning they can be easily adapted to any weakly ordered data types. The Radix Sort, however, uses the bitwise representation of the data and some bookkeeping to determine ordering, limiting its scope. Plus, it seems to be slightly more complex to implement than other sorting algorithms. For these reasons, the Radix Sort is not so used and this is where my project comes into play!
My project
My project is to implement a reusable C++ library with a clean interface that uses Radix Sort to sort a distributed (or not) array using MPI (if distributed). The project focus on distributed arrays using MPI but the library will most probably also have a serial efficient version of Radix Sort. The goal is that the library allows users to sort any data type as long as they can forgive a bitwise representation of their data. If the data are not originally integers or reals, they will have the possibility to provide a function returning a bitwise representation of their data.
Challenge
The time has come to make the announcement! I will soon launch a challenge, with a gift card for the winner, which simply consists in implementing a sorting algorithm that can sort faster than mine, if you can… A C++ code will be given with everything and a Makefile, your unique action: fill in the sorting function. Open to everybody, the only rule: be creative. Can you defeat me?
All information concerning the challenge in my next blog post so stay tuned! I am looking forward to tell you more about it.
See you soon



