Results On Performing Hadron Spectroscopy With LQCD

Welcome to my third and final blog post. At the end of the previous post, I briefly explained the goals of this project. I talked about making LQCD simulations to extract a pion mass and find an input quark mass that would give a pion mass value close to the experimental one. Of course, all of these are once again ambiguous so let me describe them step by step.
What Is Hadron Spectroscopy?
In QCD theory, almost every problem has to do with the calculation of various physical quantities using the path integral. However, those integrals are what perturbative techniques fail to calculate, which forces us to use the LQCD formalism. In our case, we will focus on a class of those problems called hadron spectroscopy. In these problems, we intend to find the mass of a hadron(e.g. a pion) based on specific input parameters.
The most essential input parameters are the gauge field configuration and the quark mass. To obtain a solution that converges with this of the path integral, we must carefully select a quark mass and conduct the same experiment with many different gauge configurations. Next, we can take the average of all outputs, which should lead to a relatively accurate solution depending on how well we chose those input parameters.
Path Towards Pion Mass Extraction
Since we discussed the necessary theoretical background, we can move forward with the procedure I followed to complete my project. Initially, I selected a quark mass equal to -0.01 and did simulations with many slightly different gauge configurations. Before you ask, yes the mass can be negative here! That happens due to an additive mass shift introduced during discretization, but it shouldn’t bother us. Also, I should clarify that all masses during the experiments are expressed in lattice units, which makes them dimensionless. That is yet another mathematical trick to make the calculations easier for the computer.
Upon completing those simulations, I extracted their pion correlators and calculated their average and standard error. A correlator is a function describing the relation of microscopic variables(e.g. spin) at different positions. The statistical observables we calculated are the key to the final step of this process. That step is to perform exponential fitting and acquire the pion mass. To achieve this, I utilized the tool called gnuplot. However, its pion mass error estimate was slightly inaccurate as it doesn’t consider the correlation among configurations. To remedy this, I replaced it by calculating the jackknife error, which is much more precise in such cases.
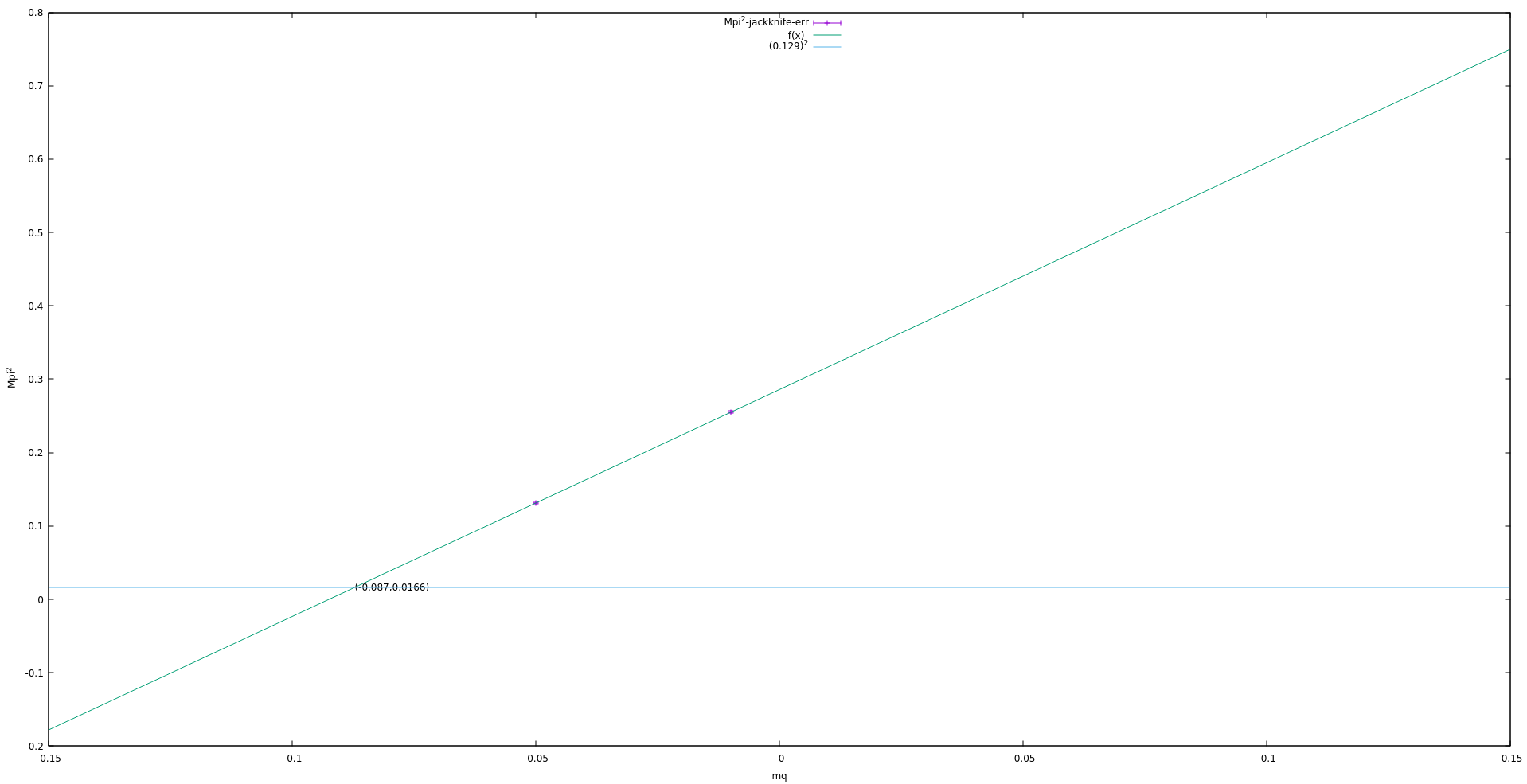
Finally, despite the already decent estimate of the pion mass value, I tried to get closer to the experimental value. That amounts to 135 MeV and translates into a lattice mass of 0.129. To this end, I exploited the approximately linear relation between the square of the pion mass and the quark mass to find an ideal target quark mass. I started by repeating the simulation with another quark mass equal to -0.05. Then, I created the line defined by the pairs we found, plugged in the desired pion mass square, and ended up with a quark mass of -0.087.
Final Results
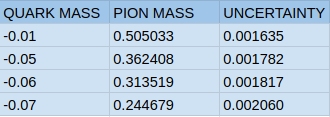
ments with 4 different quark masses
Using such a low quark mass as -0.087 dramatically increased the complexity of the underlying linear systems, and the solvers in chromaform struggled to make the solutions converge. For this reason, the lowest mass I could try was equal to -0.07, though it still provided a satisfactory outcome as seen in Figure 3. If there was more time, I would probably search for the solution to this problem by modifying other aspects of the chromaform tool (e.g. the precision, max number of iterations of linear system solvers), but this can be an interesting future project!
A Journey That Came To An End
As all of us know, every good thing ends one day. Reaching the end of my journey with PRACE SoHPC, I reflect on the whole experience and consider it one of the most precious moments in my academic life. During the program, I learned many new things and broadened my horizons. It is an undeniable fact that PRACE SoHPC is a worthwhile experience, which I suggest to everyone.
P.S. Don’t forget to check the following video presentation we made with my colleague Christopher Kirwan about the project. Also, I strongly recommend checking out Christopher’s really interesting work about benchmarking with Kokkos API.
