The HIPbit, or There and Back Again


Figure 0: Me, travelling around the reserach center with my Tesla K40 GPU.
Forschungszentrum Jülich is quite an interesting place to work at. You can think of it as a town in the middle of nowhere where over the half of the population are scientists or technicians. The research center even has its own fire department and healthcare center! It is also surrounded by chain link fences with barbed wires, which are probably designed to keep the wildlife on the outside and the researchers on the inside. To get in you have to present your personal ID card and you ought to have it on your person at all times. The security of the facility appears to be quite high on the priority list. The whole place reminds me of Black Mesa Research Facility, but with less headcrabs. I’m not even sure if I was allowed to take photos, but I did anyway.

Figure 1: My field of view while strolling around. There are lots of these bizarre solar paneled boxes all over the facility. Nobody I have asked knew what they are. Maybe it’s some on-going experiment.
You can actually spend quite a lot of time just strolling around the research center. A couple of Master students I share the office with were kind enough to take me on a tour around the campus on a route called The Two Towers. This route visits the two largest radio towers the center has. As you might deduce from the its name, the route is almost as long as the trek from Shire to Mordor. But walking isn’t all I do! I also eat brunches, lunches and second breakfasts while drinking copious amounts of coffee. In addition, during breaks from all of that stuff, I have this pretty cool programming project I’m working on.
The project is basically about calculating gravitational or electric potentials caused by groups of discrete point masses or charges on a graphics card very quickly. These sorts of potentials are encountered for example, when simulating molecular dynamics, behaviour of plasma or formation of a solar system. You want the calculations to be very fast, because simulations usually require an immense number of time steps before they’re of any use. And lastly, we want to utilize GPUs, because nowadays they’re ubiquitous and offer the cheapest FLOPSs.
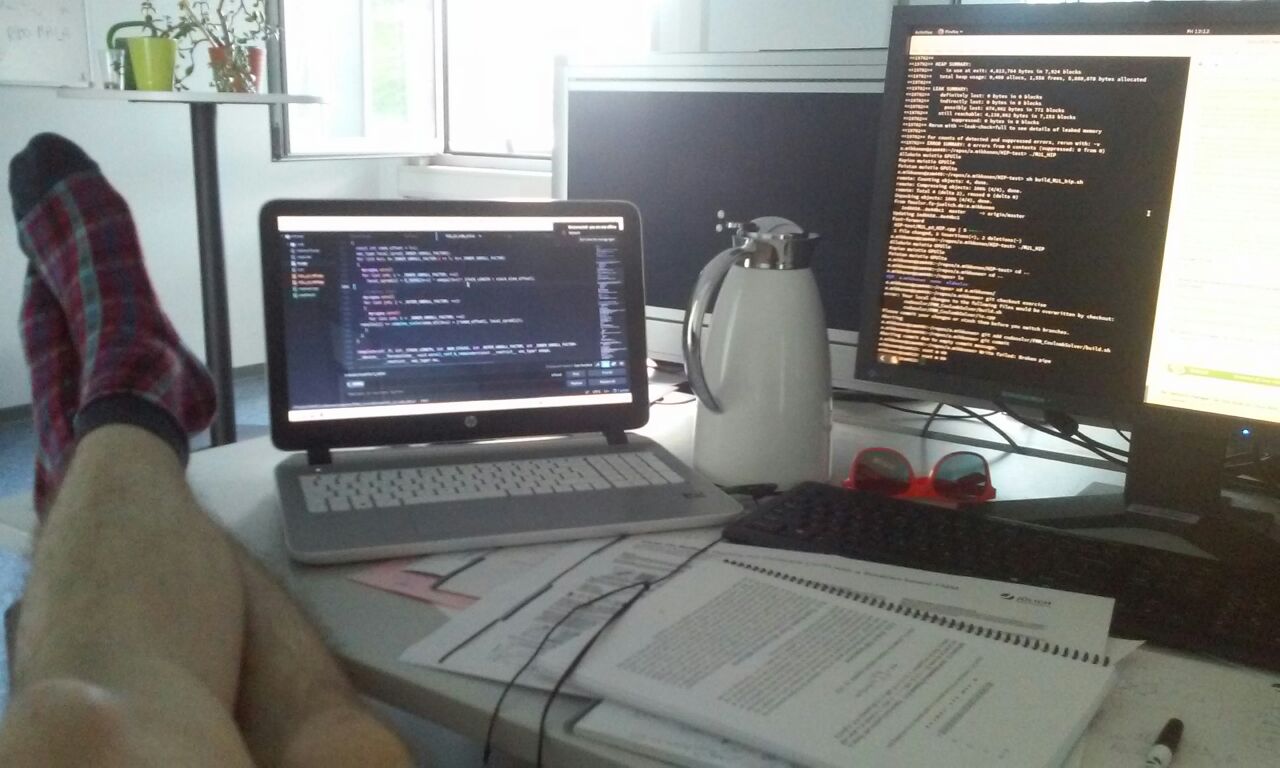
Figure 2: My field of view during a break from the strolling around. Walking’s serious business: note the legs in an optimal resting position. That white thing right there is my personal coffee kettle. That’s right, a liter of coffee, just for me!
More specifically, I convert existing CUDA code for nVidia GPUs to a more general, open-source framework called Heterogenous-Compute Interface for Portability, or HIP. With it, you only need to write source code and during compilation you decide which hardware to use. The framework is quite new and under heavy development, which becomes apparent when Googling the various error messages and noting the absence of hits from StackOverflow. In such cases, you need to do the figuring out by yourself! However unreasonable it may sound, this playing in the background has kept me sane while debugging my code.
The algorithm used for the potential computation is called the Fast Multipole Method. The large distribution of point charges (or masses) is divided into small boxes, each of which contains only several particles. The particles of a certain box and its neighbouring boxes interact classically using the usual formula for 1/r potentials and this is called the near-field. Everything further away is considered to be in the far-field. As it turns out, one can give an exact estimate of the potential outside of one particular box in the far-field with an infinite series of spherical harmonics. This we can of course approximate by selecting just a few first terms from the infinite sum. The more further away we are from the source of the potential, the more neighbouring boxes are included in the spherical harmonics series. By this one weird trick you can reduce the time complexity of this problem from quadratic to linear!
The coolest thing is that in some cases, this gives a more accurate result than the classical pointwise calculation of the potentials, by reducing the amount summations and thus diminishing the cumulative floating point addition error! No wonder the algorithm is said to be one of the most important algorithms of the last century.

Most flops a hobbit ever had! Nice story.
Thanks! No amount of flops is enough to satiate my hunger for even more!
Antti,
How can you survive in a city half filled with scientist? Isn’t this a weird place?
It is quite weird. You have lots of eccentric people all around. That’s why it’s only half-filled: the non-scientist half takes care of all practical issues.
At the gates, do they ask you ‘What has it got in its pocketses, eh?’
PS: I was standing on Brandywine bridge recently 😉
Most likely they do but I can’t be sure since German is all Elvish to me.
That’s cool! Did the place have an adventure-inducing feel to it?