Thermal conductivity of a crystal for dummies

Hi there! If you are here it is probably because you read my previous blog posts or perhaps you are in search for a tutorial on how to calculate the thermal conductivity of a crystal… in any case you are in the right place, because in the following I will explain the simulations I performed for my Summer of HPC project ‘Computational atomic-scale modelling of materials for fusion reactors‘. To understand the context of these simulations I would highly suggest reading by previous blog post if you’re interested.

First of all we need to understand what thermal conductivity is. Usually expressed with the letter ‘k’ the thermal conductivity of a material is a measure of the ability of that material to conduct heat, and is defined by the Fourier’s law for heat conduction q=-k ∇T, where q is the heat flux and ∇T the temperature gradient.
A material with an high thermal conductivity has an high efficiency in the conduction of heat, and that’s why it is important that a material like Tungsten has an high thermal conductivity for its application in a nuclear fusion reactor.

How can we calculate the thermal conductivity of a material? The relatively easiest way is to do it experimentally, applying an heat flux to the material and calculating the resulting temperature gradient; but this approach does not allow to investigate the effect of vacancies and defects at an atomic level, and that’s what we are interested in, since this defects while be formed by neutron bombardment.
And it’s here that molecular dynamics simulations come into place, with an atomistic simulations it is in fact possible to recreate this kind of configurations and investigate how they effect the thermal conductivity of the material. But first we need a reference value, so the the thermal conductivity of a perfect Tungsten crystal must be computed.

To do so in this project the LAMMPS code has been used, and the simulations have been performed on MareNostrum supercomputer of the Barcelona Supercomputing Center (BSC).
A parallelepiped simulation box is defined and Tungsten atoms are placed in a body centered cubic (BCC) crystalline structure, then an equilibration run is performed at a given system temperature, we used 300K to compare the results with previous papers. To have a constant temperature system LAMMPS uses a modified version of the equation of motion, the procedure goes under the name of Nose-Hoover algorithm.
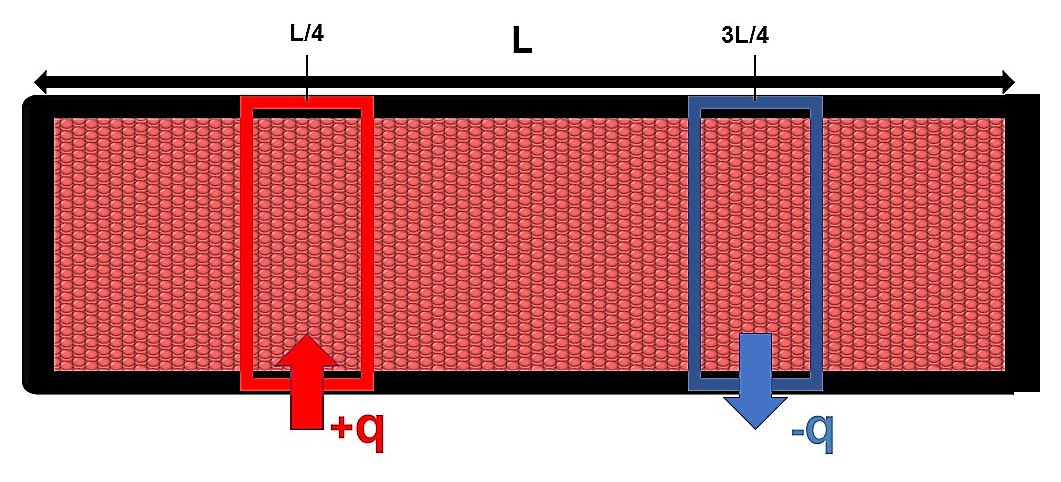
Once equilibrium is reached two regions are defined along one direction of the simulation box, at equal distance from the box borders and of equal volume, using an appropriate command a positive heat flux q starts heating one of the two regions, while an equal but negative heat flux –q starts cooling the other one.

In this way the average temperature of the system stays constant, but the first region will locally have an higher temperature while the second one a lower one, we then have a temperature gradient ∇T between these two regions; knowing the value of the heat flux q and calculating ∇T we obtain the value for the thermal conductivity k from the Fourier’s law.
This procedure has been performed using different potentials and system sizes obtaining results agreeing with previous papers.

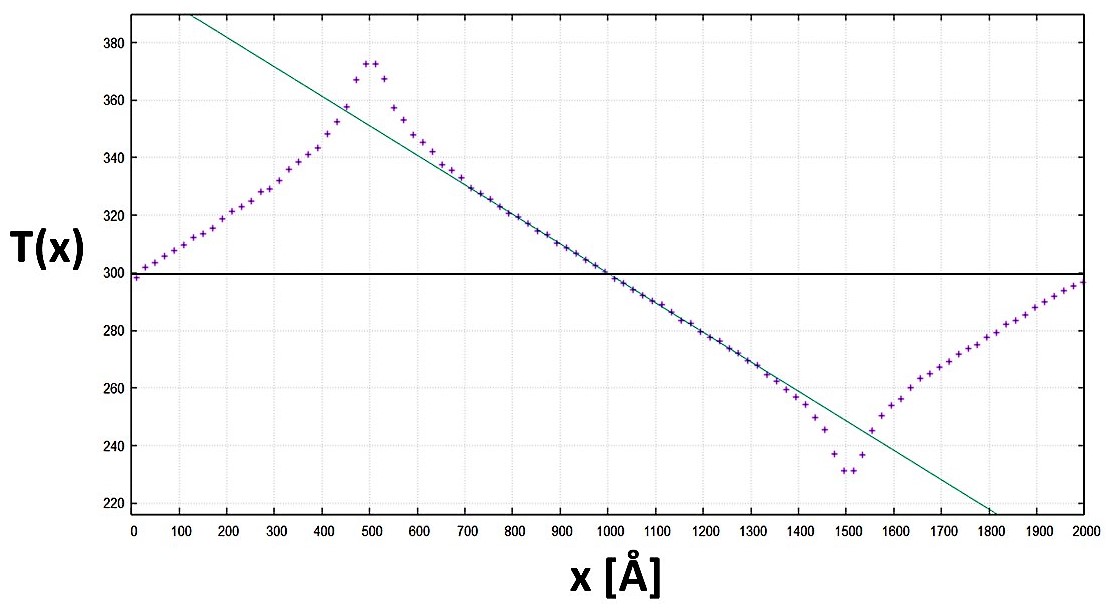
We then proceeded to add an empty bubble at the center of the system with radius r, resembling the damage caused by neutron bombardment, and repeated the same procedure obtaining a new result for the thermal conductivity of the system.
We investigated the relative variation of the thermal conductivity with respect to the value for a perfect crystal increasing the size of the empty sphere at the box center; the obtained result is a decreasing linear behaviour of the thermal conductivity as a function of the transverse (with respect to the heat flux direction) area of the sphere πr² ; the result is shown in the following graph. For high radius spheres we start to see the effect of the finite size of the simulation box, which is not infinite, and the behaviour shifts away from the linear one.

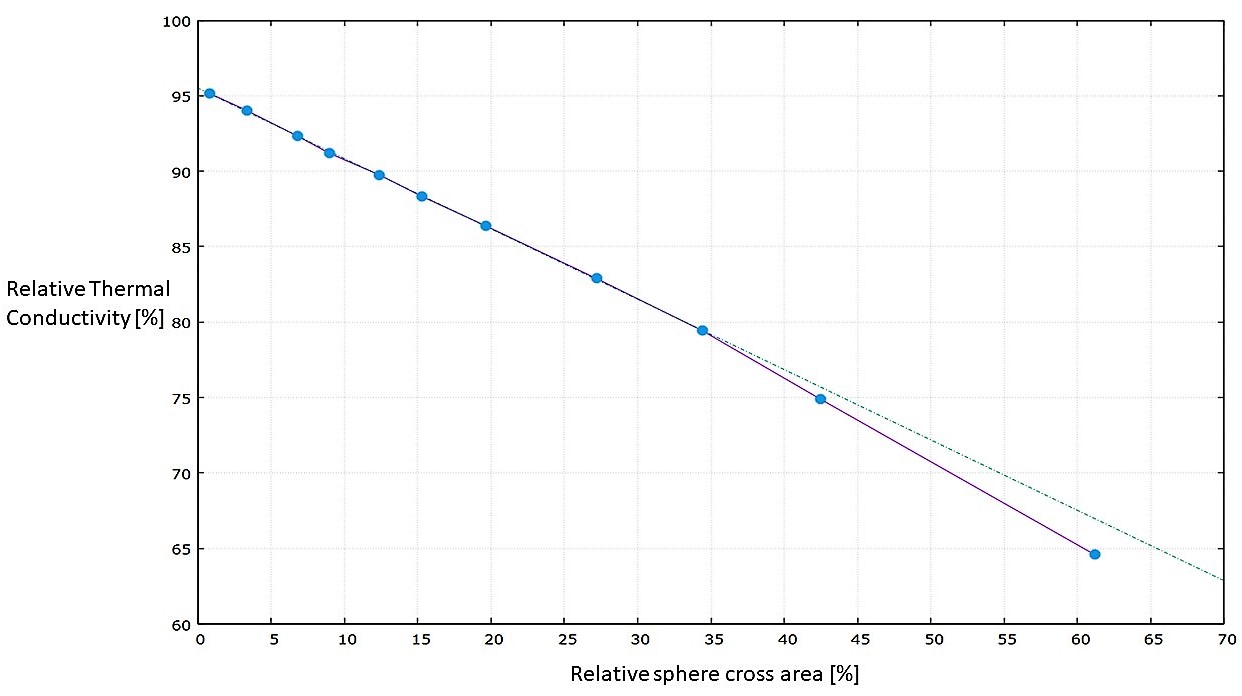
These vacancies have an important effect on a crystal system like this one, to give you an idea the first point of the graph corresponds to the removal of 11 atoms from an half million atoms system, and the thermal conductivity already drops by 5%; this is the same reason why it is so crucial to study and understand the effect that these vacancies cause on a system, since these structures will be formed also in real life conditions with real effects.
The results obtained in this project can be used as a basis to further explore this type of defects, for example injecting inside the empty bubbles Hydrogen or Helium atoms, resembling what really happens when this atoms escape from the nuclear fusion reactor core.

I’m really grateful to every person that made my partecipation for the Summer of HPC 2021 possible, it has been a wonderful experience, learning new computational skills and techniques and meeting amazing people; it is a fantastic experience that I would recommend to anyone interested in computational science and its applications.
I hope you found my blog pages interesting and helpful, if so you will sure like the posts my colleague Eoin did on the formation of defect cascades. Have a wonderful day!