To get it right you need to know what is going wrong

In previous episodes …

Hi again, in the last post I explained to you the problem we are gonna address (predicting the orientation in images of galaxies), the motivation to address this issue, the technologies we are going to use, and the way we are generating our data. Now I’m gonna be a bit more technical and explain more in detail what model we choose, how it works, and how we are going to analyze the outputs to measure its performance.

Let’s begin with the basics

To do the actual predictions we are going to use a deep neural network, as we are treating with images the best option is to choose a convolutional neural network (or CNN for short). A CNN is based on applying a series of different convolutions on each layer. In case you are curious, convolutions are a kind of “filters” that are based on matrix multiplications as shown in figure 1. This convolutions then extract more complex features as we advance in the network to end up with a general knowledge of what features the orientation of the galaxy is based on.

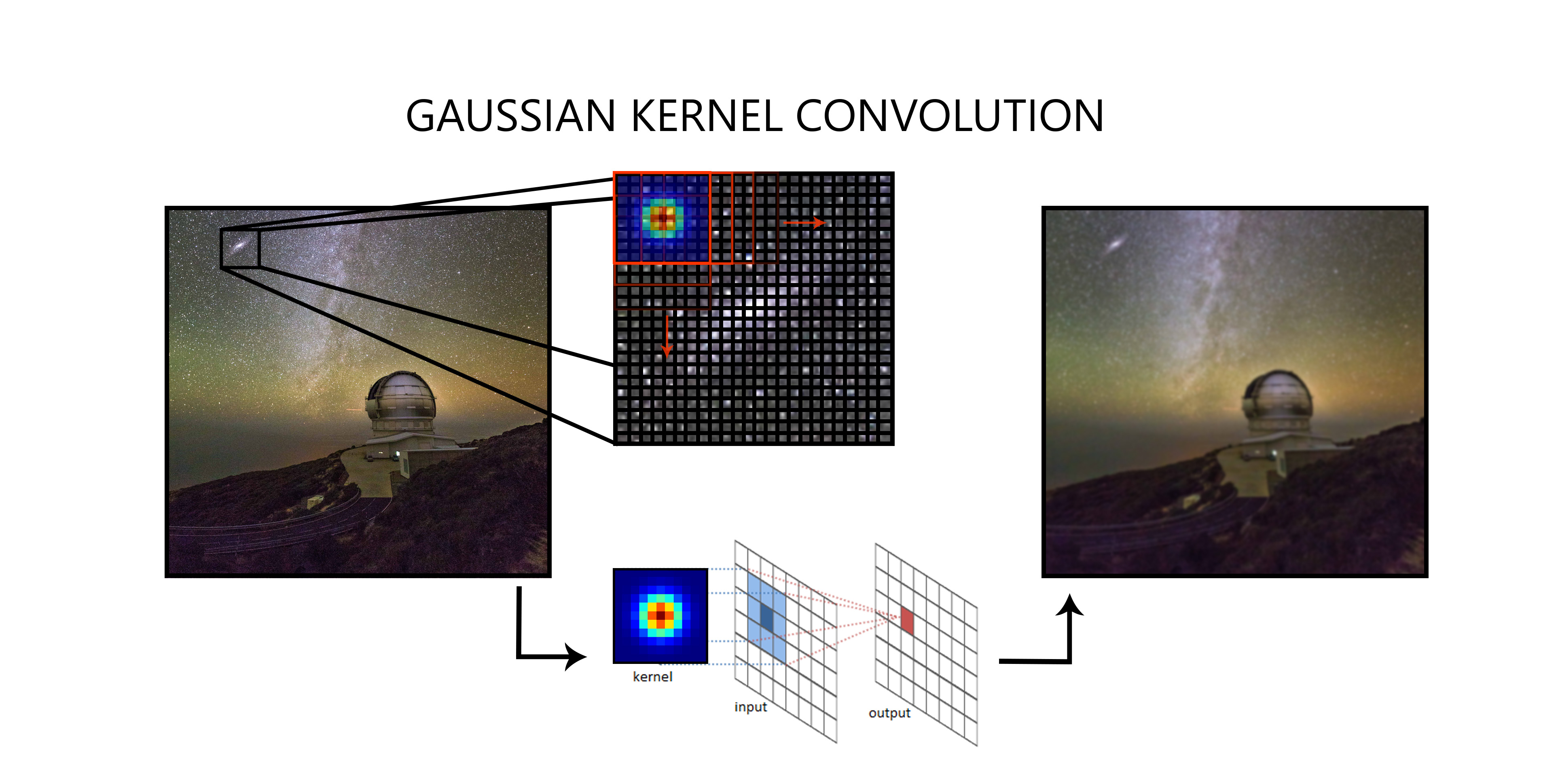
A well-trained network is one that has figured out what the correct kernels should be to extract the information that we want. For example, in the first layer, the low-level features are extracted (like edges, corners… etc) then in the successive layers more high-level information is extracted (like combine edges and corners to have an understanding of general shapes) to finally have an understanding of what the orientation of a galaxy is. If we train the network we will end up with a bunch of convolutions that have been trained to extract the most useful features and will output as a result a 2D vector that represents the projected orientation of the galaxy into the image plane.

Time to do the heavy lifting

Now that we know the basics it’s time to choose the correct architecture for the network and with the right parameters. As we have time constraints and developing a new architecture from scratch it’s a really complicated task, we will use an already existing network. We first chose RESNET to do the job (we also considered ALEXNET). We chose these networks for being a state of the art networks treating with images but since our problem is not image classification (we don’t have categories) we need to adapt them a bit. For that purpose, we add a couple of extra layers at the end to adapt the networks to our needs of predicting continuous values.

Also, we need to develop routines to visualize the results, preprocess the data (shuffle it, batch it, and multiply it by applying flips and rotations).

Knowing how wrong you are is the first step to get it right

Okay now that we know what architecture to use, how we are gonna prepare our data, and how to visualize the results, seems that is almost done right? Well … of course is not that simple.

One key aspect of training a neural network it’s defining what is wrong and what is right and in a classification model, it’s a rather easy task since we have categories between which we need to choose. In a model like ours, in which we need to predict a real parameter (in fact 2 in this case), things get a bit trickier.

We need to make a function that tells not if we are wrong or not, but by how much we are wrong. This gets even worse since we have multiple solutions for the orientation of a galaxy as the direction of the angular momentum vector can go in both directions of the orientation (axis of rotation) of the galaxy as shown in Figure 2. How we define how far is our model from reality then?

The approach we chose (as we are treating with vectors is to use the Cosine Similarity ( https://en.wikipedia.org/wiki/Cosine_similarity ) basically it’s a measure of the angular distance of the two vectors but taking into account that a +180º vector is a valid solution. It is computed with the dot product and the magnitude of the vectors A and B as:

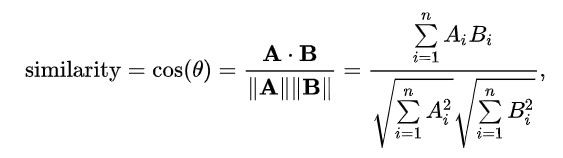
From there we began a battle to obtain an accurate metric to train the network. Stay tuned to see what the results of this amazing journey are … See you on the finish line.