Yup, that’s me. You’re probably wondering how I got into this situation…

Hello there, I’m Valentin Trophime from Grenoble in France. I study computer science in Evry (in the south of Paris) at Télécom SudParis. I will graduate next year with a specialization in distributed services. More personally, in life, I like several things but the best are probably video games (Celeste, Hollow Knight, Overwatch, Super Smash Bros or Sekiro for instance) and movies (The Big Lebowski, Hot Fuzz, Matrix, Promare, The Lord of the Ring). Also I really love think about mathematical problems especially when they are directly connected with computer science. For instance I found fascinating all the questions behind decidability and computability (this one is classic but really nice). I’m curious about those and that’s why I am here in this summer of HPC program in a project of treewidth algorithms in graph theory. In this blog I will show you an introduction to this project from my perspective.
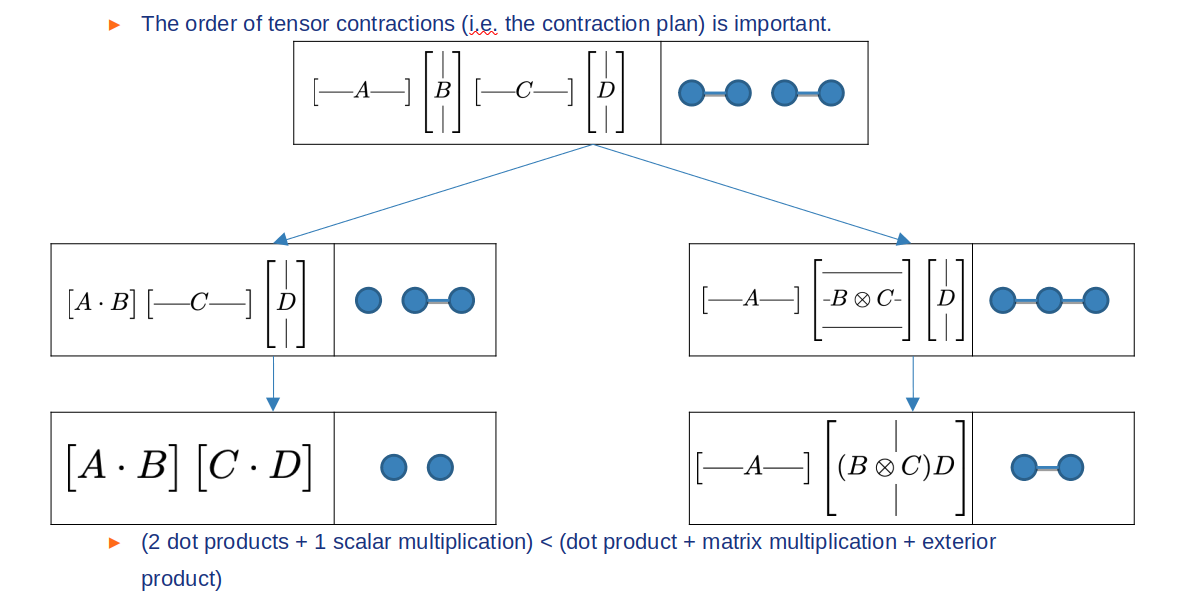
Our project is motivated by the need of simulating a quantum computer. In order to evaluate the performances of real quantum computers we need to compare them to “what we expected”. This expectation is the result of the simulation of the virtual quantum computer inside a classic computer. Simulating such a computer is done by contracting a tensor network this is basically a great multiplication of tensors of different dimensions. There are many orders possible ways to compute this multiplication and some are more efficient than others. For instance consider this simple expression with 4 vectors, these 2 ways of doing the computation don’t need the same amount of basic arithmetic operations. The first (left) order is better because it needs less computations.
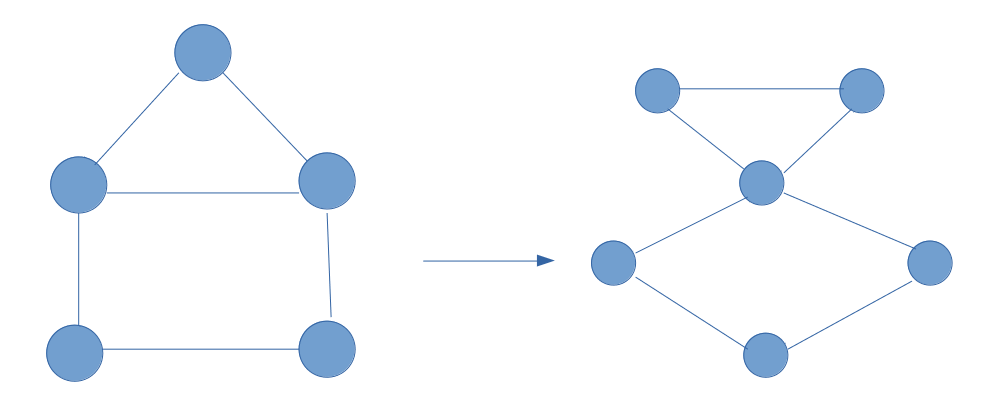
These expressions can be represented as graphs as you can see in the previous picture. The terms (tensors) of the multiplication are nodes and their degree is equal to their dimension. For instance an isolated vertex is a scalar, a vertex with 1 neighbor is a vector, with 2 neighbors a matrix and so on… Finding the best order for contraction is equivalent to considering the line graph (i.e the reversed graph, edges become vertices and new vertices are connected if their respective edges in the original graph share one vertex) and find the approximate treewidth (definition here, but for short it’s just a number to know if our graph is similar to a tree) using the process of elimination. I know this sounds like magic, the first time but with some drawing it will make more sense. Consider this tensor network graph, first we will create its line graph.
Now it’s time to calculate its approximate treewidth with elimination, basically this process is the following: for a given order of vertices delete them in order but when you delete a vertex you connect all of his neighbors together, the approximate treewidth is the maximum degree (number of neighbors) of all nodes when they are deleted. Let’s try on our example, I will choose an arbitrary order (top to bottom, left to right) like so.
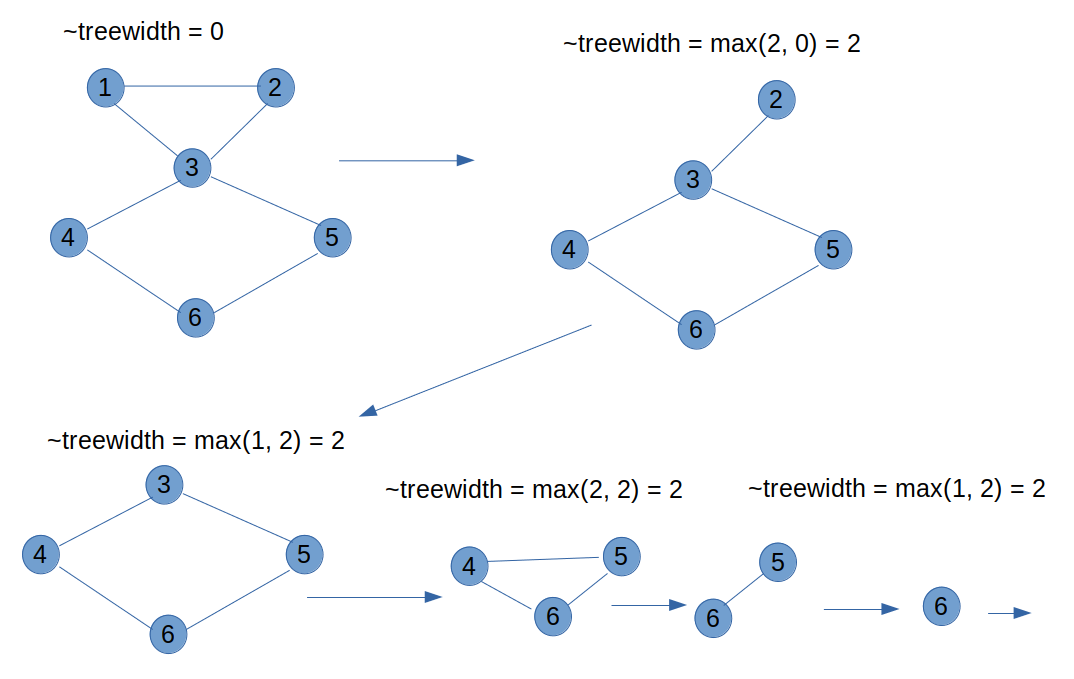
This is not rigorously the treewidth because the real one is the minimum of those approximations (for all possible orders). Testing all the orders is obviously too long in term of computation time, if the graph has N vertices, there are N! possibilities. This is known as an NP problem that’s why we usually try to compute approximation or even upper/lower bound and not the real value of the treewidth. Some approximations are based on heuristics or on complex algorithms like quickBB to guess the right order that gives the best answer. That’s why, in the beginning of our project, we will try to implement heuristics before some of the complex algorithms described in papers like this one. Our final goal is to implement those complex algorithms in a julia package with parallelization and optimization when it is possible. I hope this introduction to algorithms of treewidth in graphs, was clear. Thanks for reading, have a nice day or night, bye !

Leave a Reply