How Is an Aerodynamics Problem Solved? From Zero to Hero in 5 Steps

This post is intended to explain, from the very basics, how to deal with aerodynamics equations, in order to then understand why HPC (High Performance Computing) systems are so relevant to this matter. My aim is that, even (and especially) if you have never studied anything about fluid dynamics or engineering in general, still it is possible for you to get what I am writing about. If you already have some solid background in these fields you may not find this very interesting…
STEP 1. Physical Principle I: Mass Cannot Arise From Nothing
As was already mentioned in my first post, the motion of any fluid is governed by some equations that predict how the flow behaves. But let’s stop for a moment: where do these equations come from?
They are nothing esoteric. They just represent basic physical laws that anyone can understand. For example, we all know that, within a closed volume, the matter cannot be created out of nothing. Or, in other words: mass must be conserved. From this fact, the following equation is obtained:
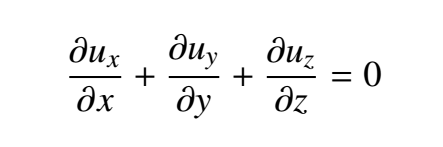
Forget about all the symbols and subscripts that you may not understand in the expression above. The only thing that you have to know is that u represents the velocity. But how is the velocity related to mass conservation? It can be understood very easily with a practical example: imagine that we have a room in which we open two doors of the same size each. Imagine that air is entering through one door and going out by the other one. If we measure the velocity of the air at both doors, we can infer how the amount of air that is inside the room is changing: if the velocity of the air that is exiting is the same as that of the air entering the room, then the amount of air inside the room must be constant. But if the velocity of the air entering is larger, then clearly air is being accumulated inside and the system is gaining mass. This is precisely what this first equation represents: it states that the mass of air inside of our room (technically called domain) depends on the velocity of the air and that if we want the mass to be constant, the velocity must fulfill some conditions for the situation to be congruent.
STEP 2. Physical Principle II: A Force Leads to an Acceleration
The next (and last) equation needed to solve the motion of a fluid is the momentum conservation. It looks as follows:
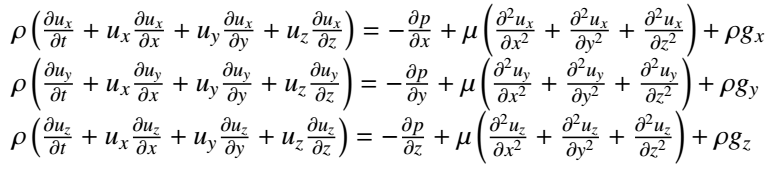
Again, forget about the nuances of the expression, they are not needed to get the main idea of how this works. Just remember that p denotes the pressure of the fluid. What these expressions are stating is just that F = m x a. Or, in other words, that the force exerted on the fluid is equal to its mass times its acceleration. As you may have noticed, this is just Newton’s second law, and it quantifies how much a given object will accelerate when a given force is applied to it. The fact that there are three equations is because the principle is applied into the three directions (x, y, z) of the 3D space, since Newton’s second law must be fulfilled in each of them (e.g. the acceleration in the x-direction must be coherent with the force provided in that direction; the same in y and z).
STEP 3. We Need as Many Equations as Unknowns
After just applying two very basic principles, the mass conservation and Newton’s second law (momentum conservation), two equations have been obtained. Now it is important to notice that, out of all the bunch of symbols that appear in those equations, in truth, there are only two quantities that are not known: the velocity u and the pressure p. That means that we have two equations and two unknowns. This is very important since having the same number of equations and unknowns means that the problem should be solvable. To put it simply: if you have x=2 and y=3, you have two equations and two unknowns, and it is evident that both the values of x and y are known. But if you have x+y=8 and y-x=2, you still have two equations and two unknowns, and it is still possible to obtain that x=3 and y=5 after just a couple of steps. In our case, the equations are more complex, but we still have two equations and two unknowns (four equations and four unknowns if we decompose the velocity in each of the directions), which means that u and p just play the role that x and y were playing right above, which in turn means that it should be possible to obtain a solution. As a matter of fact, knowing the values of the velocity and the pressure is enough to fully define the flow, at least in this case, since other properties of the flow such as the density or the viscosity are known to be approximately constant and do not need to be solved.
However, there are still some things that do not make much sense. The solution that one may expect for a fluid dynamics / aerodynamics problem is not just a value of the velocity such as u=3. What we would like to know is the value of the velocity and the pressure at every single point of the space! If we managed to obtain that, we would know for example the value of the pressure of the fluid right over each point of the surface of our body (the formula car in this case). Since the pressure is just the force divided by the surface (p = F / S → F = p x S), and the surface of the car is something that we know (we know how our car is), we could then use F = p x S and get the force that the fluid is exerting on the car at each point. Then we could sum the force at each of these points lying on the car surface to get the total force that the fluid is exerting on our car, which is the final objective. In fact, this is an important point: whereas fluid dynamics is concerned with the motion fo the fluid, aerodynamics is a subfield specifically dedicated to the computation of the forces that the fluid exerts on a body.
But the problem remains the same: how do we obtain the values of the pressure and the velocity at many points, instead of getting just an overall value? If, for example, we want to know the pressure value at 1000 different points on the car surface, that means that there are indeed 1000 unknowns, which means that we need 1000 equations! But we do not have 1000 physical laws that we can use to get more equations; the physical laws that can be applied to this problem are just two of them and have already been used up. So how could we proceed?
STEP 4. How Do We Get a Thousand Equations (or More)?
Pay attention now, cause here comes the key step that we need to understand. At the beginning of the article, we said that, as an example, we could imagine that we were solving the flow in a room, and that taking into account how much air was entering and leaving the room by the two doors, an equation could be found in terms of the velocity, to ensure that mass was conserved. Now imagine that the room is divided into two parts, which are separated by an imaginary wall that lets the air go through (one of the doors lies at each part of the room), and imagine that we are also able to measure the flow velocity at that imaginary wall, as we did at the doors. Now we can find an equation for the velocity of the flow in part 1 of the room, which will be obtained by taking into account the velocity of the flow that is entering by the door that is in that part of the room, and the velocity that is leaving the part 1 of the room towards part 2 through the imaginary wall, and by stating that mass must be conserved in that part 1 of the room. It is just the same as before, but now we are just considering half of the room, and air enters by the door and leaves towards the other part of the room through the imaginary wall. And a similar procedure can be followed for part 2 of the room. This would also be applicable to Newton’s second law, which implies that we now are able to obtain two equations for each part of the room, thanks to the fact that the physical principles are not only true for our whole domain, but also for any subdivision of it (at least if subdivisions are reasonable…).

After that process of dividing into two parts the room has been finished and the equations have been obtained, solving all the equations (which is possible, since we still have a number of equations which is equal to the number of unknowns) would give us a value of the pressure and the velocity at each of the parts of the room. So, if we want 1000 values, we just need to divide our room/domain into 1000 small parts, usually called cells. The process of diving the domain into small cells is called discretization.
STEP 5. But How Is This Related to High-Performance Computers?
The fact is that, in truth, we do not need those 1000 cells. We need many more, in the order of hundreds of millions (100 000 000). And we do not want to get the values just once, we want to solve it probably several hundreds of times, each one at a time instant, in order to see how those values of the velocity and the pressure evolve as time goes by. So we are now in the order of ten thousands of millions (10 000 000 000). And if we take into account that the number of operations that the computer has to solve just to get a single value of the pressure and the velocity at a single cell at a single time instant is large (i.e. you have seen the complexity of the equations, they were not anywhere near x+y=8 and y-x=2), then the total number of operations that the computer has to solve to get the final result could be something around 1 000 000 000 000, or what is the same, one of the former UK billions. You may start to discover why, even if a regular laptop is a decent machine, it may not be enough to solve this kind of problems.
Essentially, supercomputing and HPC systems are based on the concept of parallelization. Simplifying, HPC systems are just computers that have a very large number of cores/processors (comping units). A processor can only be doing one thing at a time (again simplifying), so the approach is the following: out of the millions of cells in which our domain was divided, a little bunch of them is given to each processor, which solves the equations for the velocity and the pressure for the cells that have been assigned to it, and then returns the results. When all the processors finish solving their respective equations, all the data is put together again and the full results are recomposed. Of course, there are a lot of details that have been omitted, like the fact that the equations that a processor is solving partly depend on the solution of the equations of other processors, which implies that very high-speed connections are needed between processors to transfer the data they need. Or the fact that a huge amount of data is handled at a time, which means that a very large RAM capacity may be needed.
6. Conclusions
I hope that this post has been useful for understanding the basic ideas of CFD simulations and the importance of HPC systems. I just wanted to point out a couple of things.
Eventually, the equations are just mathematical tools that help us express those common-sense physical principles in a way such that a solution can be found. Nothing more and nothing less than that. If you are not versed in mathematics or engineering, there is not much interest in trying to understand them literally. Understanding the principles behind them can also be very useful to grasp a general idea.
Regarding HPC, I hope the text has transmitted how important its development is in order to push the boundaries of science and technology. Not all progress will come from HPC, but without HPC development, progress will be much harder.
————————————————————————————————————–
Ahora, ¡en español!
Este artículo tiene la intención de explicar, desde lo más básico, cómo tratar con las ecuaciones que controlan la aerodinámica, para luego entender por qué los sistemas HPC (High Performance Computing – Computación de Alto Rendimiento) son tan relevantes para este asunto. Mi objetivo es que, incluso (y especialmente) si nunca has estudiado nada sobre dinámica de fluidos o ingeniería en general, aún resulte entendible. Si ya tienes estudios en estos campos, puede que no te resulte muy interesante …
PASO 1. Principio físico I: la masa no puede surgir de la nada
Como ya mencioné en mi primera publicación, el movimiento de cualquier fluido se rige por algunas ecuaciones que predicen cómo se comporta el flujo. Pero paremos por un momento: ¿de dónde vienen estas ecuaciones?
No son nada esotérico. Simplemente representan leyes físicas básicas que cualquiera puede entender. Por ejemplo, todos sabemos que, dentro de un volumen cerrado, la materia no se puede crear de la nada. O, en otras palabras: la masa debe ser conservada. De este hecho, se obtiene la siguiente ecuación:
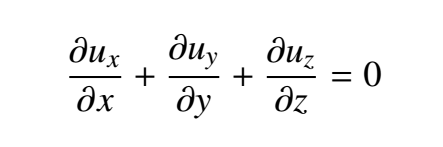
Olvídate de todos los símbolos y subíndices que no entiendas en la expresión anterior. Lo único que tienes que saber es que u representa la velocidad. Pero ¿cómo se relaciona la velocidad con la conservación de masa? Se puede entender con un ejemplo práctico: imagina que tenemos una habitación en la que abrimos dos puertas, del mismo tamaño cada una. Imagina que el aire entra por una puerta y sale por la otra. Si medimos la velocidad del aire en ambas puertas, podemos deducir cómo está cambiando la cantidad de aire que hay dentro de la habitación: si la velocidad del aire que sale es la misma que la del aire que entra, entonces la cantidad de aire dentro de la habitación está claro que será constante. Pero si la velocidad de entrada del aire es, por ejemplo, mayor, entonces se está acumulando aire en el interior y el sistema está ganando masa. Esto es precisamente lo que representa esta primera ecuación: establece que la masa de aire dentro de nuestra habitación (técnicamente llamada dominio) depende de la velocidad del aire que entra y que sale, y que si queremos que la masa sea constante, la velocidad debe cumplir algunas condiciones para que la situación sea congruente.
PASO 2. Principio físico II: una fuerza conduce a una aceleración
La siguiente (y última) ecuación necesaria para resolver el movimiento de un fluido es la conservación del momento. Se ve de la siguiente manera:
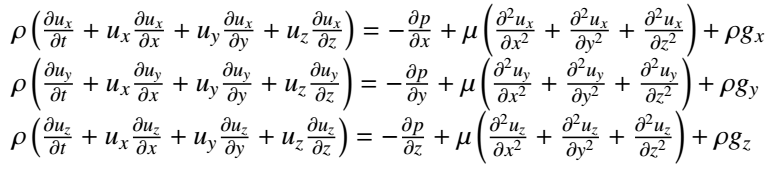
Olvídate otra vez de los detalles de la ecuación, no son necesarios para entender la idea principal de cómo funciona esto. Solo recuerda que p denota la presión del fluido. Lo que dicen estas expresiones es simplemente que F = m x a. O, en otras palabras, que la fuerza ejercida sobre el fluido es igual a su masa multiplicada por su aceleración. Como quizá habrás notado, esto es simplemente la Segunda Ley de Newton, y cuantifica cuánto acelera un objeto cuando se le aplica una fuerza determinada. El hecho de que haya tres ecuaciones se debe a que el principio se aplica en las tres direcciones (x, y, z) del espacio 3D, ya que la segunda ley de Newton debe cumplirse en cada una de ellas (por ejemplo, la aceleración en la dirección x debe ser coherente con la fuerza proporcionada en esa dirección; lo mismo en y; lo mismo en z).
PASO 3. Necesitamos tantas ecuaciones como incógnitas
Después de solo aplicar dos principios muy básicos, la conservación en masa y la segunda ley de Newton (conservación del momento), hemos obtenido dos ecuaciones. Ahora es importante darse cuenta de que, de todos los símbolos que aparecen en esas ecuaciones, en realidad solo hay dos cantidades que no conocemos: la velocidad u y la presión p. Eso significa que tenemos dos ecuaciones y dos incógnitas. Esto es muy importante ya que tener el mismo número de ecuaciones e incógnitas significa que el problema debería poder resolverse. ¿Por qué es esto cierto? En un ejemplo rápido: si x = 2 e y = 3, tenemos dos ecuaciones y dos incógnitas, y es evidente que ambos valores de x e y son conocidos. Pero si tenemos x + y = 8 e y-x = 2, todavía tenemos dos ecuaciones y dos incógnitas (aunque algo menos sencillas), y por lo tanto todavía se puede resolver: obtenemos que x = 3 e y = 5 después de solo un par de pasos. En el caso del fluido, las ecuaciones son más complejas, pero todavía tenemos dos ecuaciones y dos incógnitas (cuatro ecuaciones y cuatro incógnitas si descomponemos la velocidad en cada una de las direcciones), lo que significa que u y p simplemente juegan el papel que x e y estaban jugando justo arriba, lo que a su vez significa que debería ser posible obtener una solución. De hecho, conocer los valores de la velocidad y la presión es suficiente para obtener la solución completa. Al menos en este caso, ya que se sabemos que otras propiedades del flujo, como la densidad o la viscosidad, son aproximadamente constantes (en otros tipos de fluidos esto puede no ser cierto).
Sin embargo, todavía hay algunas cosas que no tienen mucho sentido. La solución que uno puede esperar para un problema de dinámica de fluidos / aerodinámica no es solo un valor de la velocidad, como por ejemplo u = 3. ¡Lo que nos gustaría saber es el valor de la velocidad y la presión en cada punto del espacio! Si lo logramos, sabríamos, por ejemplo, el valor de la presión del fluido justo sobre cada punto de la superficie de nuestro cuerpo (el coche de fórmula en este caso). Como la presión es solo la fuerza dividida por la superficie (p = F / S → F = p x S), y la superficie del coche es algo que conocemos (sabemos cómo es nuestro coche), podríamos usar F = p x S y obtener la fuerza que el fluido ejerce sobre el coche en cada punto. Entonces podríamos sumar la fuerza en cada uno de estos puntos que se encuentran en la superficie del coche para obtener la fuerza total que el fluido ejerce sobre nuestro coche, que es el objetivo final. De hecho, este es un punto importante: mientras que la dinámica de fluidos se relaciona con el movimiento del fluido, la aerodinámica es un subcampo específicamente dedicado al cálculo de las fuerzas que el fluido ejerce sobre un cuerpo.
Pero el problema sigue siendo el mismo: ¿cómo obtenemos los valores de la presión y la velocidad en muchos puntos, en lugar de obtener solo un valor general? Si, por ejemplo, queremos saber el valor de la presión en 1000 puntos diferentes en la superficie del coche, eso significa que hay 1000 incógnitas, ¡lo que significa que necesitamos 1000 ecuaciones! Pero no tenemos 1000 leyes físicas que podamos usar para obtener más ecuaciones; las leyes físicas que se pueden aplicar a este problema son solo dos de ellas y ya las hemos usado. Entonces, ¿cómo podríamos seguir?
PASO 4. ¿Cómo obtenemos mil ecuaciones (o más)?
Presta atención ahora, porque aquí viene el paso clave que hay que entender. Al comienzo del artículo, dijimos que, como ejemplo, podríamos imaginar que estábamos resolviendo el flujo en una habitación, y que teniendo en cuenta la cantidad de aire que entraba y salía de la habitación por las dos puertas, se podía escribir una ecuación que depende de la velocidad, para garantizar que se conserve la masa. Ahora imagina que la habitación está dividida en dos partes, que están separadas por una pared imaginaria que deja pasar el aire (después de partirla en dos, una de las puertas se encuentra en cada lado de la habitación), e imagina que también somos capaces de medir la velocidad del flujo en esa pared imaginaria, como hacíamos en las puertas. Ahora podemos obtener una ecuación para la velocidad del flujo en la parte 1 de la habitación, que se obtendrá teniendo en cuenta la velocidad del flujo que entra por la puerta que está en esa parte de la habitación, y la velocidad del fluido que sale la parte 1 de la habitación hacia la parte 2 a través de la pared imaginaria. Como la masa debe conservarse en esa parte 1 de la habitación (es decir, la cantidad de masa en la parte 1 debe ser igual a la masa que había, más la que entra, menos la que sale), podemos escribir una ecuación igual que la de antes, pero que se aplica solo a la parte 1 de la habitación. Y se puede seguir un procedimiento similar para la parte 2 de la habitación. Esto también sería aplicable para el otro principio, la segunda ley de Newton, lo que implica que ahora podemos obtener dos ecuaciones para cada parte de la habitación, un total de 4. Esto es gracias al hecho de que los principios físicos no solo son verdaderos para todo nuestro dominio, sino que también para cualquier subdivisión.

Después de ese proceso de división en dos partes, tenemos cuatro incógnitas que averiguar, la velocidad y la presión en cada una de las dos partes de la sala. ¿Es posible resolver este problema? Sí, ya que tenemos una cantidad de ecuaciones que es igual al número de incógnitas. Al resolverlo, obtendremos el valor de la presión y la velocidad en cada una de las partes de la habitación: entonces, si queremos 1000 valores, solo necesitamos dividir nuestra habitación / dominio en 1000 partes pequeñas, generalmente llamadas celdas. El proceso de dividir el dominio en celdas pequeñas se llama discretización.
PASO 5. Pero, ¿cómo se relaciona esto con los ordenadores de alto rendimiento (sistemas HPC)?
Lo cierto es que, en verdad, no necesitamos esas 1000 celdas. Necesitamos muchos más, del orden de cientos de millones (100 000 000). Y no queremos obtener los valores solo una vez, queremos resolverlo probablemente varios cientos de veces, para diferentes instantes de tiempo, para ver cómo evolucionan esos valores de la velocidad y la presión a medida que pasa el tiempo. Así que ya estamos en el orden de diez miles de millones (10 000 000 000). Y si tenemos en cuenta que la cantidad de operaciones que el ordenador tiene que resolver para obtener un solo valor de la presión y la velocidad en una sola celda y en un solo instante de tiempo es grande (se puede ver la complejidad de las ecuaciones, no se parecen a x + y = 8 e y – x = 2…), entonces el número total de operaciones que el ordenador tiene que resolver para obtener el resultado final podría ser alrededor de 1 000 000 000 000, o lo que es lo mismo, un billón. Puedes empezar a ver por qué, incluso si un portátil normal es una máquina decente, puede que no sea suficiente para resolver este tipo de problemas.
Esencialmente, los sistemas de supercomputación y HPC se basan en el concepto de paralelización. Simplificando, los sistemas HPC son solo ordenadores que tienen una gran cantidad de núcleos / procesadores (unidades de cálculo). Un procesador solo se puede hacer una cosa a la vez (simplificando), por lo que el enfoque es el siguiente: de los millones de celdas en las que dividimos nuestro dominio, se da un pequeño grupo de ellas a cada procesador, que resuelve las ecuaciones para la velocidad y la presión de las celdas que se le han asignado y luego devuelve los resultados. Cuando todos los procesadores terminan de resolver sus respectivas ecuaciones, todos los datos se vuelven a unir y se recomponen los resultados completos. Por supuesto, hay muchos detalles que omito, como el hecho de que las ecuaciones que un procesador está resolviendo dependen en parte de la solución de las ecuaciones de otros procesadores, lo que implica que se necesitan conexiones de muy alta velocidad entre procesadores para transferir los datos que necesitan. O el hecho de que se maneja una gran cantidad de datos a la vez, lo que significa que se necesita una gran capacidad de RAM.
6. Conclusiones
Espero que este artículo haya sido útil para comprender las ideas básicas de las simulaciones de CFD y la importancia de los sistemas HPC. Solo quería añadir un par de cosas.
Al final, las ecuaciones son solo herramientas matemáticas que nos ayudan a expresar esos principios físicos de sentido común, de tal manera que se pueda encontrar una solución. Nada más y nada menos que eso. Si no has estudiado matemáticas o ingeniería, no hay mucho interés en tratar de entenderlas literalmente. Comprender los principios detrás de ellas también puede ser muy útil para hacerse una idea general del tema.
Con respecto al HPC, espero que el texto haya transmitido cuánto de importante es su desarrollo para ampliar los límites de la ciencia y la tecnología. No todo el progreso vendrá del HPC, pero sin el desarrollo del HPC, el progreso será mucho más difícil.
