If your problem is too big, get a GPU to do the work!

Hello again, it is time to update you on my project and since Marc already told you what lattice Quantum Chromodynamics is about we can dive right in.

To deal with QCD, we take a four dimensional space-time lattice and let it evolve step by step until it can be considered to be in thermal equilibrium and then take a snapshot every n-th or so step to get a set of lattices (called a Markov chain) to do measurements on.

So why does this require supercomputing?

Well, to start with, we are not satisfied with just using a small lattice. Nature happens to take place in a continuum and the introduction of a lattice also introduces errors, which get worse as you take smaller grids. So lets take something reasonable like a size of 8 for each space dimension and 24 for the time (which still is quite small). That way you already have 12288 points and on each of those lives a Dirac spinor of another 12 complex-numbered entries. Now, to let the lattice evolve, we need to, as always, calculate the inverse of a matrix, which contains the interactions between all points. So this is some kind of 147456×147456 monstrosity (called the Dirac matrix), which is thankfully sparse (we only consider nearest neighbor interactions). Oh, and all of this needs to be done multiple times per evolution step. So supercomputing it is.

But to deal with the above, we still need to introduce some trickery. For example, one could notice that you can distinguish between even and odd lattice sites like on some strange, four-dimensional chess board. Then you only interact by nearest neighbor with sites of the same color, which allows you to basically halve the Dirac matrix and deal with even and odd sites separately.

Also, you do not save the entire Dirac matrix, only the interactions between neighbors. These are described by SU(3) matrices, which are quite similar in handling to the 3D rotation matrices your gaming GPU uses to rotate objects in front of your screen. With the introduction of general purpose GPUs, this probably has become an exclusively historic reason, but it sure helped to get some speed up in the early days.

But we talked enough now, lets look at some speedups!

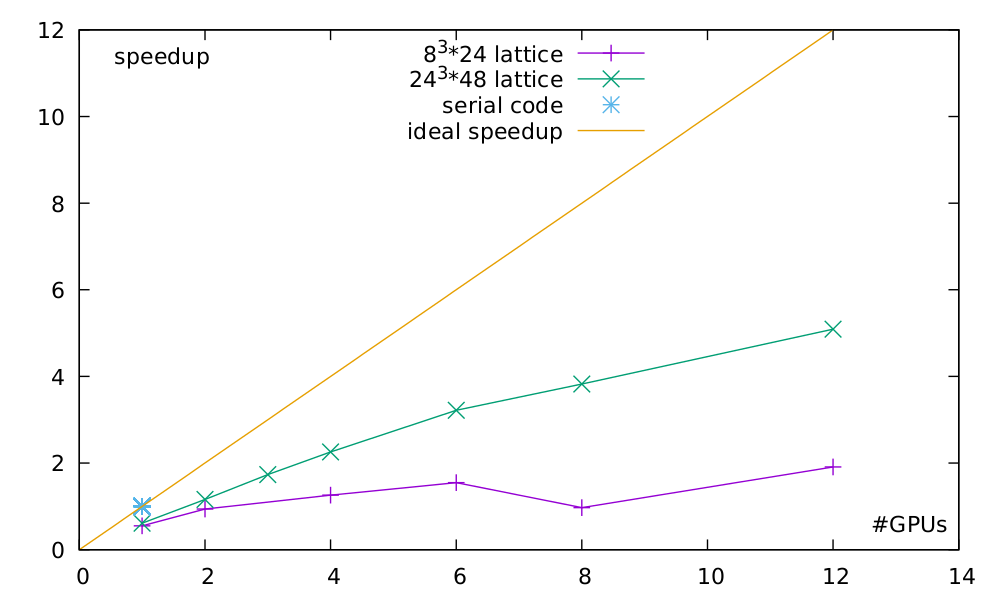
Speedup comparison between a smaller and a medium sized lattice.

As you can see, using parallel code is quite pointless for small lattices. It even gets worse at eight GPUs since you need to have a second dimension parallelized to support that many nodes (Yes, distributing 24 sites on 8 nodes would still work, but you need an even number of sites on each node.). But lo and behold, look at the speedup once we use a reasonable sized lattice. This is how we like it. Not a perfect speedup, of course, but sufficiently working and just waiting to be tuned.

So lets see how well this baby performs at the end of the summer and stay tuned for the next update!