Studying the smallest particles with the biggest machines

Hi everyone! Welcome back! It’s has been three weeks since we arrived in Nicosia. As an introduction to Cyprus culture, our site coordinator (shout-out to Stelios!) took us out for a meze the night we landed. I’ve never seen so many dishes for just 3 people! On top of that, everything tasted amazing, specially the halloumi, a mixture of goat and sheep cheese which is usually served grilled.
On the next day, we went around the old part of Nicosia (inside the Venetian walls), and it was quite difficult to find our way, since it looked like a labyrinth. But now we know it like the palm of our hand. Also, who would have known that the usage of Greek letters in physics problems would turn out to be really useful (even though we don’t understand Greek).

Fig. 1: Walking route marker found around the old part of Nicosia. Notice the shape of the Venetian Walls.
Back to work. As I mentioned in the introductory post, here I’m going to explain what my project is about and what I’ll have to do. But on second thought I’m going to give you guys a little bit of background.
First of all, we need to know a bit of physics (don’t be scared). In school, we all learned that there are 4 fundamental forces that govern how particles interact with each other: gravity, electromagnetism, strong and weak. The one that I’m interested in is the strong interaction, and the theory behind it is called Quantum Chromodynamics (or QCD).
With only two ingredients, quarks and gluons, QCD tries to explain a wide range of phenomena: from the collisions taking place at LHC (very high energy, around the TeV scale) to how the protons and nucleons are squeezed together to form the nucleus of the atoms (very small energy, around the MeV scale). The problem is that, while for the first case we can manage to understand the process using pen and paper, for the second one it is very difficult, since all our mathematical tools break down at this energy regime.
This obstacle has not stopped physicists from making predictions at this scale, even though they can no longer be from first principles and depend on experimental data. If we want to use QCD directly and compute (for example) how the mass of the proton emerges from the interaction between the quarks and the gluons, the only way to do it is by using computers. Or, to be more precise, supercomputers.
To do that, we need to program QCD on a computer. This has been known for a couple of decades: lattice QCD (LQCD). It has the word lattice in it because what we do is discretize the space-time in a 4-dimensional grid, placing the quarks on the nodes of this lattice and the gluons on the links. Then, if we want to simulate the proton, we put 3 quarks (2 up and 1 down quarks) on the lattice, let them evolve, and see if at the end we get a proton or not. But why is it so computationally demanding? We have to evaluate a path integral, or in other words, we have to compute every possible path that a quark can take from one point of the lattice to each and every other. And then repeat this computation several times to get enough statistics.
As an example, in Fig. 2, the masses for different baryons (particles made up of 3 quarks, like the proton) have been calculated by different collaborations, and then compared with experimental data:
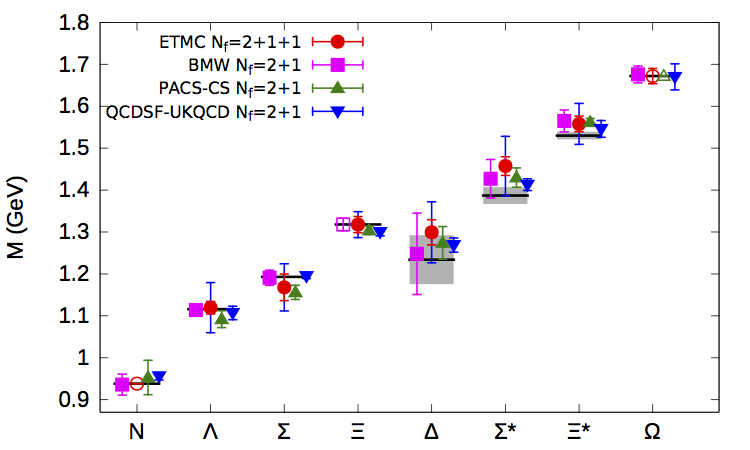
Fig. 2: The colored points are the masses of the baryons computed using LQCD, and the black line (with gray band) is the experimental value [1].
One of these is the multigrid solver. To know what it is you’ll have to wait for the next post, where I’ll also introduce my project. See you then!
References:
- C. Alexandrou, V. Drach, K. Jansen, C. Kallidonis and G. Koutsou. “Baryon spectrum with Nf=2+1+1 twisted mass fermions“. Phys. Rev. D 90, no. 7, 074501 (2014) [arxiv:1406.4310 [hep-lat]]
