Parallel boundary point method
Project reference: 1520
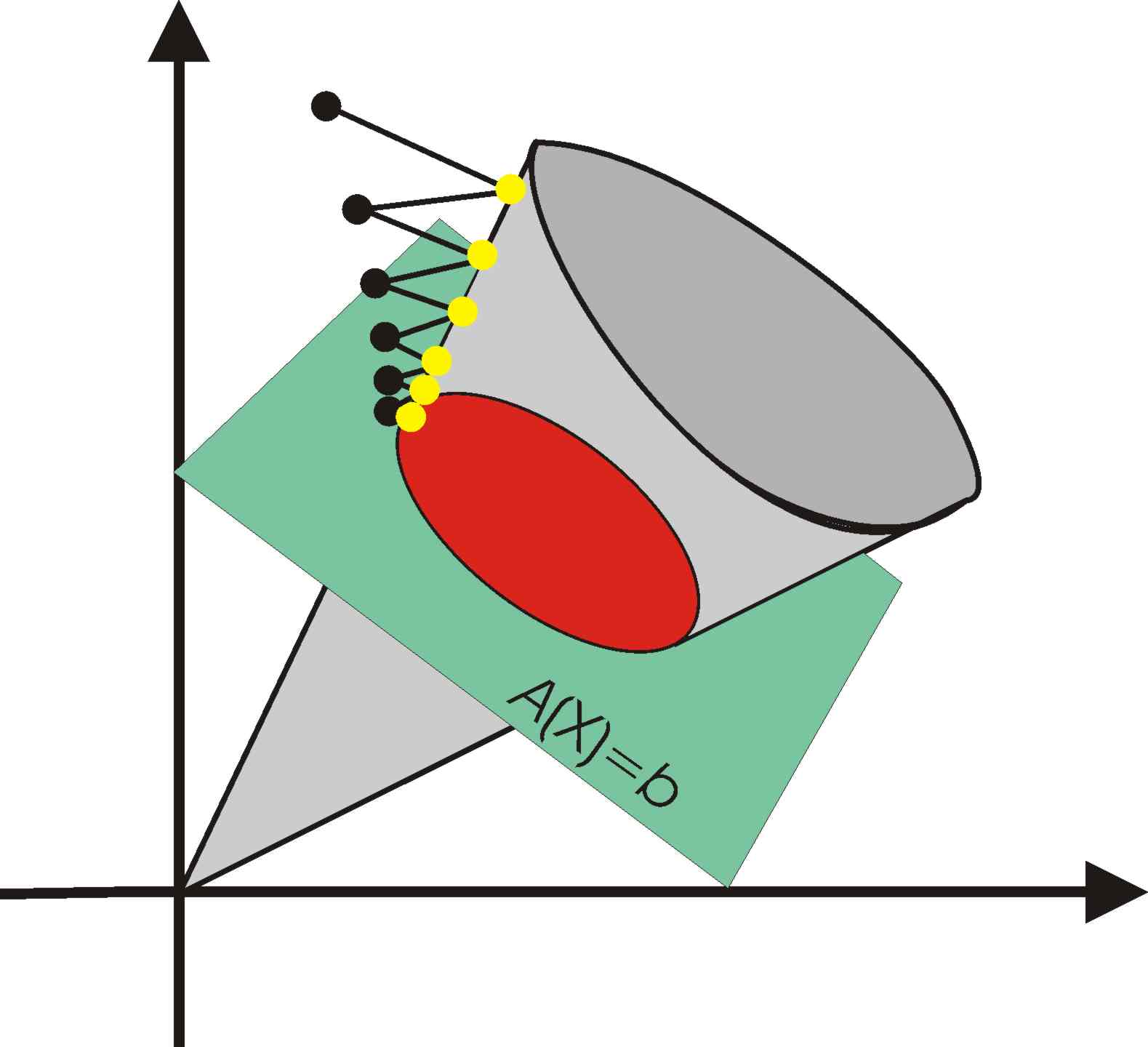
Semidefinite programming problems are optimization problems where we look for a symmetric matrix that satisfies certain set of linear equations, is positive semi definite (has all eigenvalues non-negative) and yields maximum value of given linear objective function (see e.g. http://en.wikipedia.org/wiki/Semidefinite_programming) .
The boundary point method has recently turned out to be a very efficient method for problems with large number of linear equations which are nearly orthogonal, see e.g. http://link.springer.com/article/10.1007%2Fs00607-006-0182-2.
The steps that define its complexity are solving a large system of linear equations and computing a spectral decomposition of block diagonal symmetric matrix in every iteration.
Both steps can be speeded up by parallelization and using HPC. We expect that the parallelized version of the method will be able to solve much larger problems regarding the number of constraints and the number of diagonal blocks and will therefore yield new challenges for other methods.
Project mentor: Janez Povh
Site Co-ordinator: Leon Kos
Learning Outcomes
A parallelised and for HPC prepared upgrade of the code available at https://www.math.aau.at/website/?page_id=94
Student Prerequisites (compulsory)
Programming in C or C++. Some linear algebra (solving systems of linear equations, computing eigenvalues and eigenvectors). Basic knowledge in optimization (at least linear programming). Understanding Matlab code.
Student Prerequisites (desirable)
Basics from non-linear optimization (semidefinite programming)
Training Materials
https://www.math.aau.at/website/?page_id=94
http://link.springer.com/article/10.1007%2Fs00607-006-0182-2.
http://www.is.titech.ac.jp/~kojima/articles/Taiwan1.pdf
Workplan
- Week 2: study of semidefinite programming and Boundary point method
- Week 2-4: coding the Boundary point method
- Week 5-6: testing the method
- Week 7-8: running the method on large instances of semidefinite programming problems and collect the results.
Final Product Description
By the product we will be able to tackle instances of semidefinite programming problems that are beyond the reach for all state-of-the-art software for these type of problems.
Adapting the Project – Increasing the Difficulty
We can consider other steps of the method for parallelization (i.e. trying many different step lengths or step directions in every iteration and taking best of them for the update of the current solution).
Adapting the Project – Decreasing the Difficulty
We can consider only the spectral decomposition which is one of the two bottle necks of the method and try to speed up only this part of the method.
Resources
https://www.math.aau.at/website/?page_id=94
http://link.springer.com/article/10.1007%2Fs00607-006-0182-2.
Organization
Faculty of information studies in Novo mesto, Slovenia


[…] 20. Parallel boundary point method […]