Quantum Teleportation: Fiction or Reality?

Teleportation might seem a fancy expression and you might think it’s only possible in fictional world. However, it’s the reality in quantum communication. No quantum information is actually being transferred between sender and receiver during the process except the must needed classical data which is sent through a classical channel.
What is quantum teleportation?
If you already read my first blog, I promised to come back again with my first month’s experience of the HPC project. By this time, I have learned two important algorithms and one protocol as an initial training. It’s quite hard to talk about all of them in this short context, so I chose to give you a quick go through about the quantum teleportation protocol.
Quantum teleportation is basically a protocol that facilitates the transfer of quantum information i.e. an unknown quantum state,
![]()
from sender to receiver. Say, the sender is named Alice and the receiver is named Bob, then the information transfer between them requires two main components:
- A source to produce an entangled qubit pair or EPR pair.
- A classical communication channel to transfer classical bits.
In case you are unfamiliar with the concept of the entangled state, it’s a quantum state such as,
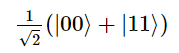
Clearly, this state has a 50% chance of being measured in the state |00⟩ and a 50% chance of being measured in the state |11⟩. The most important implication of such a state is that measuring one qubit will tell us the state of the other as the superposition collapses immediately after measurement. For example, if we measure the top qubit and get the state |1⟩, the overall state of the pair would be:
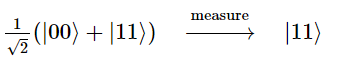
Why such implication is significant for quantum teleportation is the fact that, even with a separation of light-years away, measuring one qubit of the entangled pair appears to have an immediate effect on the other. Now let us focus on the protocol itself. A schematic is presented below.

An animation showing quantum teleportation [Credit: Source].
So you can see, both Alice(Source) and Bob(Destination) receives an entangled qubit pair (AB). Alice then performs some operations(Bell state measurement) on her end and sends the results to Bob over a classical channel. Upon receiving the classical information, Bob then performs some more operations on his end and finally has the state D. Let’s now look more closely what’s happening in each box.
What’s inside the black boxes?
We will now build the quantum circuit for the protocol in step-by-step. The fundamental components for any quantum circuit are quantum gates. Our protocol needs four single-qubit gates, which are, Hadamard gate, CNOT gate, X gate and Z gate. I would suggest you to look here to know more about quantum gates.
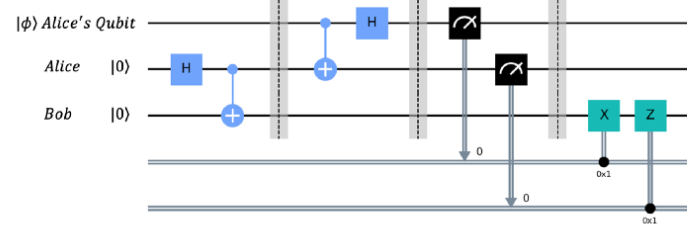
Let’s go through the following steps and see how the circuit is built.
Step 1: The first step is to create an EPR pair of the qubits of Alice and Bob. It is done before the first dotted barrier by applying a Hadamard gate followed by a CNOT gate.
Step 2: In this step, Alice applies two gates (CNOT followed by a Hadamard gate) on both the state |φ⟩ and her own qubit. For the application of CNOT, |φ⟩ acts as control qubit and Alice’s qubit acts as target qubit.
Step 3: Now Alice applies measurement on both the qubit to be transmitted and her own qubit. She then stores the outcome in two classical bits and send them to Bob through classical channel.
Step 4: Depending on the classical bits Bob receives from Alice, he now applies following operations on his qubits:
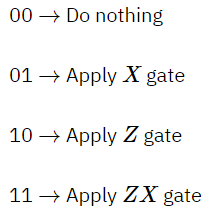
And finally!! The state Bob receives is exactly the one Alice had. And that’s how the protocol enables a piece of quantum information to be sent to a distant receiver. If you are further interested about the mathematical proof whether the state Bob receives is the same state |φ⟩ or not, you can give this a read.
I hope you learnt something interesting. Please do let me know in comments if you have any questions. I am yet to talk about my findings for this project. So, check my upcoming blogs if you want to learn more exciting stuffs about quantum algorithms.
